题目内容
已知A、B、M三点不共线,对于平面ABM外任意一点O,若
+
=3
-
,则点P与A、B、M( )
| OB |
| OM |
| OP |
| OA |
| A、共面 | B、共线 |
| C、不共面 | D、不确定 |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:
+
=3
-
,可化为
=
+
+
,根据四点共面的向量表示法,可得答案.
| OB |
| OM |
| OP |
| OA |
| OP |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OM |
解答:
解:∵A、B、M三点不共线,
故A,B,M三点共面,
又∵对于平面ABM外任意一点O,若
+
=3
-
,
则
=
+
+
,
∵
+
+
=1,
故点P与A、B、M共面,
故选:A
故A,B,M三点共面,
又∵对于平面ABM外任意一点O,若
| OB |
| OM |
| OP |
| OA |
则
| OP |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OM |
∵
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故点P与A、B、M共面,
故选:A
点评:本题考查的知识点是四点共面的向量表示法,当A、B、M三点不共线,
=a
+b
+c
,a+b+c=1?P与A、B、M四点共面.
| OP |
| OA |
| OB |
| OM |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
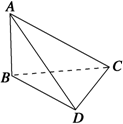 如图,在四面体ABCD中,AB=1,AD=2
如图,在四面体ABCD中,AB=1,AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
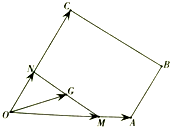 如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=
如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=