题目内容
如图是一个几何体的三视图,则该几何体的表面积是( )


A、98+3
| ||
B、98+6
| ||
C、88+3
| ||
D、88+8
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图知几何体的上部是三棱锥,下部是长方体,且长方体的长、宽、高分别为4、4、4;三棱锥的高为2,为等腰三角形,求出各个面的面积,相加可得答案.
解答:
解:由三视图知几何体的上部是四棱锥,下部是长方体,
且长方体的长、宽、高分别为4、4、4,
故长方体的各个面的面积均为:4×4=16,
三棱锥的底面面积为:
×4×4=8,
三棱锥的三个侧面面积为:
×4×2
+2×
×2
×2=8
,
故该几何体的表面积:S=6×16-8+8
=88+8
,
故选:D
且长方体的长、宽、高分别为4、4、4,
故长方体的各个面的面积均为:4×4=16,
三棱锥的底面面积为:
| 1 |
| 2 |
三棱锥的三个侧面面积为:
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
故该几何体的表面积:S=6×16-8+8
| 5 |
| 5 |
故选:D
点评:本题考查了由三视图求几何体的表面积,解题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
相关题目
已知双曲线C:4x2-my2=4m(m>0)的一条渐近线方程为2x-3y=0,则双曲线C的焦距为( )
A、2
| ||
| B、6 | ||
C、2
| ||
| D、4m |
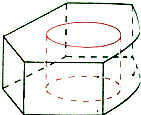 有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?
有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)? 一几何体如图所示,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,CB=CD=CF.
一几何体如图所示,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,CB=CD=CF.