题目内容
若椭圆mx2+ny2=1(m>0,n>0)与直线x+y-1=0交于A,B两点,若
=
,则过原点与线段AB的中点M的连线的斜率为 .
| n |
| m |
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由直线x+y-1=0,可得y=-x+1代入mx2+ny2=1得:(m+n)x2-2nx+n-1=0,利用韦达定理,确定M的坐标,即可求出利用过原点与线段AB中点的直线的斜率.
解答:
解:由直线x+y-1=0,可得y=-x+1代入mx2+ny2=1得:(m+n)x2-2nx+n-1=0,
设A、B的坐标为(x1,y1),(x2,y2),则有:x1+x2=
,y1+y2=1-x1+1-x2=2-(x1+x2)=
∴M的坐标为:(
,
),
∴过原点与线段AB的中点M的连线的斜率为
=
.
故答案为:
.
设A、B的坐标为(x1,y1),(x2,y2),则有:x1+x2=
| 2n |
| m+n |
| 2m |
| m+n |
∴M的坐标为:(
| n |
| m+n |
| m |
| m+n |
∴过原点与线段AB的中点M的连线的斜率为
| m |
| n |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查直线与椭圆的位置关系,考查韦达定理的运用,解题的关键是直线与椭圆方程的联立.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
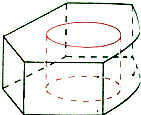 有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?
有一堆规格相同的铁制(铁的密度是7.8/cm3)六角螺帽(如图)共重5.8kg,已知底面是正六边形,边长为12mm,内孔直径为10mm,高为10mm,问这堆螺帽大约有多少个(π取3.14,可用计算器)?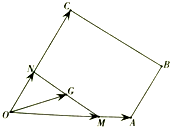 如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=
如图,梯形OABC中,OA=OC=2AB=1,OC∥AB,∠AOC=