题目内容
18.设正项数列{an}的前n项和Sn满足6Sn=an+12-9n(n∈N*),且a2,a3,a5构成等比数列,则数列{an}的通项公式为 an=3n-3.分析 根据数列的递推公式可得数列{an}为公差为3的等差数列,再根据a2,a3,a5构成等比数列,即可求出通项公式.
解答 解:∵6Sn=an+12-9n,
当n=1时,6a1=a22-9
当n≥2时,6Sn-1=an2-9(n-1)
∴6an=an+12-9(n-1)-an2+9(n-1)
∴an+12=an2+6an+9=(an+3)2,
∵an>0,
∴an+1=an+3,
∴数列{an}为公差为3的等差数列,
∴an=a1+3(n-1),
∵a2,a3,a5构成等比数列,
∴a32=a2•a5,
∴(a1+6)2=(a1+3)(a1+12)
解得a1=0,
∴an={an}3n-3,
∴a2=3,
∴满足6a1=a22-9,
∴an=3n-3,
故答案为:3n-3
点评 本题考查了数列的递推公式和和通项公式的求法,考查了学生分析问题解决问题的能力,属于中档题

练习册系列答案
相关题目
8.某社区超市购进了A,B,C,D四种新产品,为了解新产品的销售情况,该超市随机调查了15位顾客(记为ai,i=1,2,3,…,15)购买这四种新产品的情况,记录如下(单位:件):
(Ⅰ)若该超市每天的客流量约为300人次,一个月按30天计算,试估计产品A的月销售量(单位:件);
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
| 顾 客 产 品 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
| A | 1 | 1 | 1 | 1 | 1 | ||||||||||
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
9.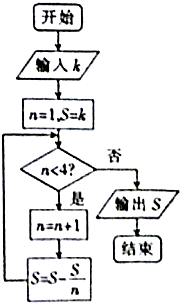 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )| A. | 4.5 | B. | 6 | C. | 7.5 | D. | 9 |
6.已知A={x|-4<x<1},B={x|x2-x-6<0},则A∪B等于( )
| A. | (-3,1) | B. | (-2,1) | C. | (-4,2) | D. | (-4,3) |
13.已知实数x,y满足$\left\{\begin{array}{l}{3x-y-7≥0}\\{5x-4y≤0}\\{y≤10}\end{array}\right.$,则$\frac{y+x}{x}$的最大值为( )
| A. | 1 | B. | $\frac{30}{17}$ | C. | $\frac{47}{17}$ | D. | 2 |
3.已知集合A={x|(x-6)(3x+8)<0},B={x|y=$\sqrt{x+1}$},则A∩B等于( )
| A. | [-1,6) | B. | (-1,6) | C. | (-$\frac{8}{3}$,-1] | D. | (-$\frac{8}{3}$,-1) |
7.已知等比数列{an}为递增数列,Sn是其前n项和.若a1+a5=$\frac{17}{2}$,a2a4=4,则S6=( )
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{63}{4}$ | D. | $\frac{63}{2}$ |
8.已知定义在R上的奇函数f(x)满足当x≥0时,f(x)=1og2(x+2)+x+b,则|f(x)|>3的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-,4)∪(4,+∞) | C. | (-2,2) | D. | (-4,4) |