题目内容
定义在R上的函数f(x)同时满足f(-x)=f(x),f(x)=f(4-x),且当2≤x≤6时,f(x)=(
)|x-m|+n
(Ⅰ)求函数f(x)的一个周期;
(Ⅱ)若f(4)=31,求m,n的值.
| 1 |
| 2 |
(Ⅰ)求函数f(x)的一个周期;
(Ⅱ)若f(4)=31,求m,n的值.
考点:函数的周期性
专题:函数的性质及应用
分析:(Ⅰ)根据函数周期的定义即可求函数f(x)的一个周期;
(Ⅱ)利用函数的奇偶性和周期性进行求值即可.
(Ⅱ)利用函数的奇偶性和周期性进行求值即可.
解答:
解:(Ⅰ)∵f(-x)=f(x),f(x)=f(4-x),
∴f(x)=f(4-x)=f(x-4),
即f(4+x)=f(x),
即4是函数f(x)的一个周期;
(Ⅱ)∵函数的周期是4,
∴f(2)=f(6),
即(
)|2-m|+n=(
)|6-m|+n,
∴|2-m|=|6-m|,解得m=4,
又f(4)=31,
∴f(4)=(
)|4-4|+n=1+n=31,
解得n=30.
∴f(x)=f(4-x)=f(x-4),
即f(4+x)=f(x),
即4是函数f(x)的一个周期;
(Ⅱ)∵函数的周期是4,
∴f(2)=f(6),
即(
| 1 |
| 2 |
| 1 |
| 2 |
∴|2-m|=|6-m|,解得m=4,
又f(4)=31,
∴f(4)=(
| 1 |
| 2 |
解得n=30.
点评:本题主要考查函数值的计算以及函数周期性的判断,要求熟练掌握函数周期性和奇偶性的应用.

练习册系列答案
相关题目
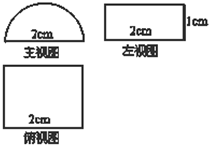 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)
已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)| A、6+2π | B、4+2π |
| C、6+3π | D、4+3π |
若对于实数a、b,定义运算“*”为:a*b=
,则函数f(x)=log2x*log
x的值域为( )
|
| 1 |
| 2 |
| A、(0,1] |
| B、(-∞,0] |
| C、[0,+∞) |
| D、[1,+∞) |
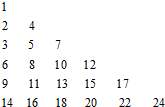 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=