题目内容
已知a=(sin2x,2cos2x-1),b=(sinθ,cosθ)(0<θ<π),函数f(x)=a•b的图象经过点(
,1).
(Ⅰ)求θ及f(x)的最小正周期;
(Ⅱ)当x∈[-
,
]时,求f(x)的最大值和最小值.
| π |
| 6 |
(Ⅰ)求θ及f(x)的最小正周期;
(Ⅱ)当x∈[-
| π |
| 6 |
| π |
| 4 |
考点:三角函数的最值,平面向量数量积的运算,三角函数的周期性及其求法
专题:计算题,三角函数的求值
分析:(Ⅰ)利用向量数量积的坐标运算易求f(x)=cos(2x-θ),从而可求f(x)的最小正周期;又y=f(x)的图象经过点(
,1),0<θ<π,可求得θ;
(Ⅱ)由(Ⅰ)得f(x)=cos(2x-
),-
≤x≤
⇒-
≤2x-
≤
,利用余弦函数的单调性可求得f(x)的最大值和最小值.
| π |
| 6 |
(Ⅱ)由(Ⅰ)得f(x)=cos(2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 6 |
解答:
解:(Ⅰ)∵f(x)=
•
=sin2xsinθ+cos2xcosθ=cos(2x-θ),
∴f(x)的最小正周期为T=π,
∵y=f(x)的图象经过点(
,1),
∴cos(
-θ)=1,
又0<θ<π,
∴θ=
;
(Ⅱ)由(Ⅰ)得f(x)=cos(2x-
),
∵-
≤x≤
,
∴-
≤2x-
≤
,
当2x-
=0,即x=
时,f(x)取得最大值1;
2x-
=-
,即x=-
时,f(x)取得最小值-
.
| a |
| b |
∴f(x)的最小正周期为T=π,
∵y=f(x)的图象经过点(
| π |
| 6 |
∴cos(
| π |
| 3 |
又0<θ<π,
∴θ=
| π |
| 3 |
(Ⅱ)由(Ⅰ)得f(x)=cos(2x-
| π |
| 3 |
∵-
| π |
| 6 |
| π |
| 4 |
∴-
| 2π |
| 3 |
| π |
| 3 |
| π |
| 6 |
当2x-
| π |
| 3 |
| π |
| 6 |
2x-
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查向量数量积的坐标运算,突出考查三角函数的周期性及其求法及余弦函数的单调性与最值,属于中档题.

练习册系列答案
相关题目
若对于实数a、b,定义运算“*”为:a*b=
,则函数f(x)=log2x*log
x的值域为( )
|
| 1 |
| 2 |
| A、(0,1] |
| B、(-∞,0] |
| C、[0,+∞) |
| D、[1,+∞) |
关于x的一元二次不等式ax2-5x-50>0的解集为(x1,x2),且x2-x1=15,则a=( )
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
利用简单随机抽样从含有6个个体的总体中抽取一个容量为3的样本,则总体中每个个体被抽到的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
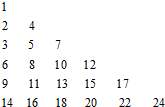 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=