题目内容
用秦九韶算法求多项式f（x）=5x5+4x4+3x3+2x2+x+1，当x=2时的值的过程中，不会出现的数值为（ ）
| A、14 | B、127 |
| C、259 | D、64 |
考点：中国古代数学瑰宝
专题：计算题
分析：用秦九韶算法可得：f（x）=（（（（5x+4）x+3）x+2）x+1）x+1，进而得出．
解答：
解：f（x）=（（（（5x+4）x+3）x+2）x+1）x+1，
当x=2时，v0=5，v1=5×2+4=14，
v2=14×2+3=31，v3=31×2+2=64，
v4=64×2+1=129，v5=129×2+1=259，
由以上可知：当x=2时的值的过程中，不会出现的数值为127．
故选：B．
当x=2时，v0=5，v1=5×2+4=14，
v2=14×2+3=31，v3=31×2+2=64，
v4=64×2+1=129，v5=129×2+1=259，
由以上可知：当x=2时的值的过程中，不会出现的数值为127．
故选：B．
点评：本题考查了秦九韶算法，属于基础题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
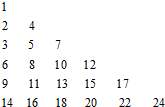把正整数按一定的规则排成了如图所示的三角形数表．设aij（i，j∈N+）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a42=8．若aij=2013，则i+j=a，b，c分别是△ABC的内角A，B，C的对边，下面能得出△ABC为锐角三角形的条件是（ ）
A、sinA+cosA=
| ||||
| B、tanA+tanB+tanC＞0 | ||||
| C、b=3，c=3，B=30° | ||||
D、
|