题目内容
2.在△ABC中,已知tanA=$\sqrt{3}$,则cos5A=$\frac{1}{2}$.分析 根据0°<A<180°,tanA=$\sqrt{3}$,可得A的值,然后代入cos5A计算得答案.
解答 解:在△ABC中,0°<A<180°,由tanA=$\sqrt{3}$,可得A=60°,
则cos5A=cos300°=cos(360°-60°)=$cos60°=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查同角三角函数的基本关系的应用,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.已知圆x2+y2+2x-2y+2a=0截直线x+y+2=0所得弦长为4,则实数a的值是( )
| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
17.若函数f(x)=x2-a|x|+a2-3有且只有一个零点,则实数a=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2 | D. | 0 |
14.在△ABC中,D在AB上,AD:DB=1:2,E为AC中点,CD、BE相交于点P,连结AP.设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$(x,y∈R),则x,y的值分别为( )
| A. | $\frac{1}{2},\frac{1}{3}$ | B. | $\frac{1}{3},\frac{2}{3}$ | C. | $\frac{1}{5},\frac{2}{5}$ | D. | $\frac{1}{3},\frac{1}{6}$ |
11.设x∈R,则“x>2”是“|x-1|>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.在△ABC中,若a=1,b=2,cosA=$\frac{2\sqrt{2}}{3}$,则sinB=( )
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
 夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.
夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.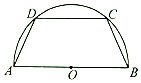 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ<$\frac{π}{2}$),L为等腰梯形ABCD的周长.