题目内容
12. 夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.
夏威夷木瓜是木瓜类的名优品种,肉红微味甜深受市民喜爱.某果农选取一片山地种植夏威夷木瓜,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的$\frac{4}{3}$倍.(1)求a,b的值;
(2)若从产量在区间(50,60]上的果树随机抽取2株果树,求它们的产量分别落在(50,55]和(55,60]两个不同区间的概率的概率.
分析 (1)样本中产量在区间(45,50]上的果树有a×5×20=100a株,样本中产量在区间(50,60]上的果树有:b+0.02)×5×20=100(b+0.02株,由此能求出a,b.
(2)产量在区间(50,55]的有4株棵树,产量在(55,60]的有2株果树,从中任取2株,基本事件总数n=${C}_{6}^{2}=15$,它们的产量分别落在(50,55]和(55,60]两个不同区间包含的基本事件个数m=${C}_{4}^{1}{C}_{2}^{1}$=8,由此能求出它们的产量分别落在(50,55]和(55,60]两个不同区间的概率.
解答 解:(1)样本中产量在区间(45,50]上的果树有a×5×20=100a(株),
样本中产量在区间(50,60]上的果树有:(b+0.02)×5×20=100(b+0.02)(株),
依题意,有100a=$\frac{4}{3}$×100(b+0.02),即a=$\frac{4}{3}$(b+0.02),①
根据频率分布直方图知(0.02+b+0.06+a)×5=1,②
由①②,得:a=0.08,b=0.04.
(2)由(1)知产量在区间(50,55]的有4株棵树,产量在(55,60]的有2株果树,
从中任取2株,基本事件总数n=${C}_{6}^{2}=15$,
它们的产量分别落在(50,55]和(55,60]两个不同区间包含的基本事件个数m=${C}_{4}^{1}{C}_{2}^{1}$=8,
∴它们的产量分别落在(50,55]和(55,60]两个不同区间的概率p=$\frac{m}{n}=\frac{8}{15}$.
点评 本题考查概率的求法,考查频率分布直方图的应用,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

| A. | ?x∈R,sinx+cosx>$\sqrt{2}$ | B. | 若0<ab<1,则b<$\frac{1}{a}$ | ||
| C. | 若x2=|x|,则x=±1 | D. | 若m2+$\sqrt{n}$=0,则m=n=0 |
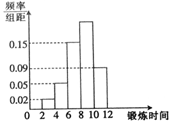 某校有150位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10)小时内的人数为( )
某校有150位教职员工,其每周用于锻炼身体所用时间的频率分布直方图如图所示,据图估计,锻炼时间在[8,10)小时内的人数为( )| A. | 30 | B. | 120 | C. | 57 | D. | 93 |
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | $\frac{{x}^{2}}{3}$-y2=1 | C. | $\frac{{x}^{2}}{2}$-y2=1 | D. | x2-$\frac{{y}^{2}}{2}$=1 |