题目内容
16.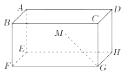 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
分析 取FG的中点N,作MO⊥EH于O,连接MN,ON,MH,OG,通过MG和平面EFGH所成角的正切值为$\frac{1}{2}$,推出$\frac{MO}{OG}$=$\frac{1}{2}$,然后求解即可.
解答  解:取FG的中点N,作MO⊥EH于O,连接MN,ON,MH,OG,
解:取FG的中点N,作MO⊥EH于O,连接MN,ON,MH,OG,
在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,可得△MNG≌△MGH,则△ONG≌△OGH,
所以ON=GH=AB=1,
因为N是FG的中点,所以NG=$\frac{1}{2}$FG=$\frac{1}{2}$AD=$\frac{1}{2}$×2=1,
所以在Rt△ONG中,OG=$\sqrt{O{N}^{2}+N{G}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$
MG和平面EFGH所成角的正切值为$\frac{1}{2}$,可得
$\frac{MO}{OG}$=$\frac{1}{2}$,则MO=$\frac{1}{2}OG$=$\frac{\sqrt{2}}{\;}2$.
则点M到平面EFGH的距离为:$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查直线与平面的所成角的求法,点到平面的距离的求法,考查转化思想以及计算能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
7.(x-1)($\frac{1}{x}$+x)6的展开式中的一次项系数是( )
| A. | 5 | B. | 14 | C. | 20 | D. | 35 |
4.m,n是不同的直线,α,β是不重合的平面,下列说法正确的是( )
| A. | 若α∥β,m?α,n?β,则m∥n | |
| B. | 若m,n?α,m∥β,n∥β,则α∥β | |
| C. | m,n是异面直线,若m∥α,m∥β,n∥α,n∥β,则α∥β | |
| D. | 若α∥β,m∥α,则m∥β |
1.$\int_{-1}^1{({sinx+\sqrt{1-{x^2}}})}dx$=( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{π}{4}$ | D. | 0 |
8.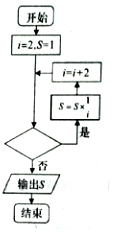 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
 如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )
如图,给出的是计算连乘数值的程序框图,其中判断框内不能填入( )| A. | i≤2019? | B. | i<2019? | C. | i≤2017? | D. | i≤2018? |