题目内容
11.双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1,F2,A为右支上一点,AF1与双曲线左支相交于点B,且$\overrightarrow{{F_1}A}=3\overrightarrow{{F_1}B},|{\overrightarrow{O{F_1}}}|=|{\overrightarrow{OA}}|$(O为坐标原点),则双曲线C的渐近线方程为y=±2x.分析 设A(m,n),B(s,t),(m,n>0,s<0,t>0),由m2+n2=c2,又$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,解得m,n,再由$\overrightarrow{{F}_{1}A}$=3$\overrightarrow{{F}_{1}B}$,F1(-c,0),运用向量共线的坐标表示,求得s,t,代入双曲线的方程,可得b=2a,进而得到双曲线的渐近线方程.
解答 解:设A(m,n),B(s,t),(m,n>0,s<0,t>0)
由题意可得m2+n2=c2,
又$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,
解得m=$\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$,n=$\frac{{b}^{2}}{c}$,
再由$\overrightarrow{{F}_{1}A}$=3$\overrightarrow{{F}_{1}B}$,F1(-c,0),
可得m+c=3(s+c),n-0=3(t-0),
即有s=$\frac{m-2c}{3}$=$\frac{1}{3}$($\frac{a\sqrt{{c}^{2}+{b}^{2}}}{c}$-2c)
t=$\frac{1}{3}$n=$\frac{{b}^{2}}{3c}$,
代入双曲线的方程可得,$\frac{(a\sqrt{{c}^{2}+{b}^{2}}-2{c}^{2})^{2}}{9{c}^{2}{a}^{2}}$-$\frac{{b}^{2}}{9{c}^{2}}$=1,
结合c2=a2+b2,化简整理,可得b=2a,
则双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±2x.
故答案为:y=±2x.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的求法,注意运用向量共线的坐标表示和点满足双曲线的方程,考查化简整理的运算能力,属于中档题.

| A. | {2,3} | B. | {3,4} | C. | {4,5} | D. | {5,6} |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |

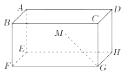 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.