题目内容
1．$\int_{-1}^1{（{sinx+\sqrt{1-{x^2}}}）}dx$=（ ）| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{π}{4}$ | D． | 0 |
分析 利用定积分的几何意义求定积分即可．
解答 解：原式=${∫}_{-1}^{1}sinxdx+{∫}_{-1}^{1}\sqrt{1-{x}^{2}}dx$=0+$\frac{1}{2}π×{1}^{2}$=$\frac{π}{2}$；
故选：A．
点评 本题考查了定积分的计算；利用定积分的几何意义也求定积分的一种计算方法．
练习册系列答案
相关题目
11．已知f（x）=$\frac{1}{2}$x+sinx，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]，则导函数f′（x）是（ ）
| A． | 仅有极小值的奇函数 | B． | 仅有极小值的偶函数 | ||
| C． | 仅有极大值的偶函数 | D． | 既有极小值也有极大值的奇函数 |
12．
一个凸多面体，其三视图如图，则该几何体的体积为（ ）
一个凸多面体，其三视图如图，则该几何体的体积为（ ）| A． | 5$\sqrt{2}$ | B． | 6$\sqrt{2}$ | C． | 9 | D． | 10 |
如图所示，游乐场中摩天轮匀速逆时针旋转，每转一圈需要6min，其中心距离地面40.5m，摩天轮的半径为40m，已知摩天轮上点P的起始位置在最低点处，在时刻t（min）时点P距离地面的高度为f（t）=Asin（wt+φ）+h（A＞0，w＞0，-π＜φ＜0，t≥0）．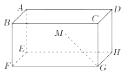
如图所示，在长方体ABCD-A1B1C1D1中，AD=2，AB=AE=1，M为矩形AEHD内一点，若∠MGF=∠MGH，MG和平面EFGH所成角的正切值为$\frac{1}{2}$，则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$．
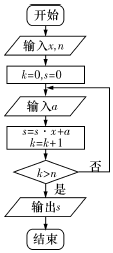中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图，执行该程序框图，若输入的x=3，n=2，依次输入的a为2，2，5，则输出的s=（ ）