题目内容
6.设数列{an}(n≥1,n∈N)满足a1=2,a2=6,且sn+2+an=sn+1+2an+1+2,若[x]表示不超过x的最大整数,则$[{\frac{2018}{a_1}+\frac{2018}{a_2}+\frac{2018}{a_3}+…+\frac{2018}{{{a_{2018}}}}}]$=2017.分析 构造bn=an+1-an,可判数列{bn}是4为首项2为公差的等差数列,累加法可得an=n(n+1),裂项相消法可得答案.
解答 解:构造bn=an+1-an,则b1=a2-a1=4,
由题意可得(an+2-an+1)-(an+1-an)=bn+1-bn=2,
故数列{bn}是4为首项2为公差的等差数列,
故bn=an+1-an=4+2(n-1)=2n+2,
故a2-a1=4,a3-a2=6,a4-a3=8,…,an-an-1=2n,
以上n-1个式子相加可得an-a1=$\frac{1}{2}$(n-1)(4+2n),
解得an=n(n+1),
∴$\frac{1}{{a}_{n}}$=$\frac{1}{n}$-$\frac{1}{n+1}$
∴$\frac{2018}{{a}_{1}}$+$\frac{2018}{{a}_{2}}$+…+$\frac{2018}{{a}_{2018}}$=2108(1-$\frac{1}{2}$+$\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{2018}$-$\frac{1}{2019}$)=2018(1-$\frac{1}{2019}$)=2018-$\frac{2018}{2019}$,
∴$[{\frac{2018}{a_1}+\frac{2018}{a_2}+\frac{2018}{a_3}+…+\frac{2018}{{{a_{2018}}}}}]$=2017,
故答案为:2017
点评 本题考查等差数列的通项公式,涉及等差数列的判定和累加法以及裂项相消法求和,属中档题.

练习册系列答案
相关题目
17.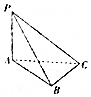 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )| A. | 4π | B. | 9π | C. | 12π | D. | 36π |
1.若函数f(x)=ln(x2+1)的值域为{0,1,2},从满足条件的所有定义域集合中选出2个集合,则取出的2个集合中各有三个元素的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
18.过圆x2+y2-8x-2y+8=0内一点P(3,-1)的最长弦,最短弦所在的直线方程式分别是( )
| A. | x-y-4=0,2x-y-7=0 | B. | 2x+y-5=0,x-2y-5=0 | ||
| C. | x-2y-1=0,2x-y-7=0 | D. | 2x-y-7=0,x+2y-1=0 |
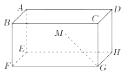 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.