题目内容
5.在△ABC中,已知$\frac{a}{tanA}=\frac{b}{tanB}$,则△ABC的形状是等腰三角形.分析 由已知利用正弦定理可求cosA=cosB,利用余弦函数y=cosx在[0,π]上单调递减,可直接得到A=B,从而可求三角形为等腰三角形.
解答 解:在△ABC中,∵$\frac{a}{tanA}=\frac{b}{tanB}$,$\frac{a}{sinA}=\frac{b}{sinB}$,
∴cosA=cosB,
∵A∈(0,π),B∈(0,π),余弦函数y=cosx在[0,π]上单调递减,
∴A=B,
则△ABC为等腰三角形;
故答案为:等腰.
点评 本题主要考查了正弦定理,余弦函数的单调性,考查了计算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.设实数x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y-4≤0}\end{array}\right.$,若对于任意b∈[0,1],不等式ax-by>b恒成立,则实数a的取值范围是( )
| A. | ($\frac{2}{3}$,4) | B. | ($\frac{2}{3}$,+∞) | C. | (2,+∞) | D. | (4,+∞) |
17.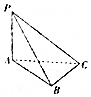 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )| A. | 4π | B. | 9π | C. | 12π | D. | 36π |
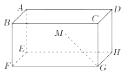 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.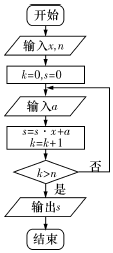 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=3,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=3,n=2,依次输入的a为2,2,5,则输出的s=( )