题目内容
7.(x-1)($\frac{1}{x}$+x)6的展开式中的一次项系数是( )| A. | 5 | B. | 14 | C. | 20 | D. | 35 |
分析 ($\frac{1}{x}$+x)6的展开式的通项公式为Tr+1=${∁}_{6}^{r}$$(\frac{1}{x})^{6-r}{x}^{r}$=${∁}_{6}^{r}$x2r-6,令2r-6=0,解得r=3;令2r-6=1,无解,舍去.即可得出.
解答 解:($\frac{1}{x}$+x)6的展开式的通项公式为Tr+1=${∁}_{6}^{r}$$(\frac{1}{x})^{6-r}{x}^{r}$=${∁}_{6}^{r}$x2r-6,令2r-6=0,解得r=3;令2r-6=1,无解,舍去.
∴($\frac{1}{x}$+x)6的展开式中的常数项为${∁}_{6}^{3}$,无一次项,
所以(x-1)($\frac{1}{x}$+x)6的展开式中的一次项系数为20,
故选:C.
点评 本题考查了二项式定理的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
17.函数y=sinx-cosx,则f'(π)的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | π |
18.随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚,车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调査,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如下的数据资料:
若由资料知y对x呈线性相关关系.试求:
1线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
2估计使用年限为10年时,车的使用总费用是多少?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 总费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
1线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
2估计使用年限为10年时,车的使用总费用是多少?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
15.设实数x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y-4≤0}\end{array}\right.$,若对于任意b∈[0,1],不等式ax-by>b恒成立,则实数a的取值范围是( )
| A. | ($\frac{2}{3}$,4) | B. | ($\frac{2}{3}$,+∞) | C. | (2,+∞) | D. | (4,+∞) |
2.已知集合A={x∈N|4x-x2≥0},B={x∈N|log2(x+1)≥2},则A∩B等于( )
| A. | {2,3} | B. | {3,4} | C. | {4,5} | D. | {5,6} |
12. 一个凸多面体,其三视图如图,则该几何体的体积为( )
一个凸多面体,其三视图如图,则该几何体的体积为( )
 一个凸多面体,其三视图如图,则该几何体的体积为( )
一个凸多面体,其三视图如图,则该几何体的体积为( )| A. | 5$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 9 | D. | 10 |
17.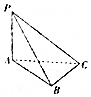 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
 如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )
如图所示,三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,AB=1,BC=PA=2,则该几何体外接球的表面积为( )| A. | 4π | B. | 9π | C. | 12π | D. | 36π |
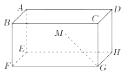 如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.
如图所示,在长方体ABCD-A1B1C1D1中,AD=2,AB=AE=1,M为矩形AEHD内一点,若∠MGF=∠MGH,MG和平面EFGH所成角的正切值为$\frac{1}{2}$,则点M到平面EFGH的距离为$\frac{\sqrt{2}}{2}$.