题目内容
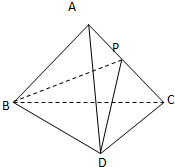 已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=
已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=| 6 |
(1)若P是AC边上的一点,当△PBD的面积最小时,求二面角P-BD-A的平面角的正切值;
(2)能否找到一个球,使A,B,C,D都在该球面上,若不能,请说明理由;若能,求该球的内接圆柱的表面积的最大值.
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)取BC之中点为O,连接AO,DO,由已知得AO⊥BC,AB⊥AC,AO⊥DO,从而AO⊥平面BCD,作PH⊥BC于H,HE⊥BD于E,连PE,则∠PEH是二面角P-BD-C的平面角,由此能求出二面角P-BD-A的平面角的正切值.
(2)取BC中点O,则OA=OB=OC=OD,存在以O为球心,半径R=
a的球,由此能求出球的内接圆柱的表面积的最大值.
(2)取BC中点O,则OA=OB=OC=OD,存在以O为球心,半径R=
| 2 |
解答:
 解:(1)取BC之中点为O,连接AO,DO,
解:(1)取BC之中点为O,连接AO,DO,
∵AB=AC=AD=2a
则AO⊥BC,又AB⊥AC,则BC=2
a,AO=
a,
在△BCD中,∵CD=
a,
则DO=
a,且sin∠CBD=
,
在△OAD中,∵AO2+DO2=4a2=AD2,则AO⊥DO,
又BC∩DO=O,且BC,DO?平面BCD,则AO⊥平面BCD
作PH⊥BC于H,HE⊥BD于E,连PE,
PH⊥平面BCD,PH⊥HE,得PE⊥BD,
则∠PEH是二面角P-BD-C的平面角,
设PH=x=CH,∴BH=2
a-x,
∴EH=
(2
a-x)=
a-
x,
∴PE=
=
=
a•
,
∵0<x≤
a,∴x=
a时,S△PBD最小,
此时PH=
a,EH=
a,则tan∠PEH=
=
,
过点O做OF⊥BD于F,连接AF,得AF⊥BD,
则∠AFO是二面角A-BD-C的平面角,
因O为BC之中点,且BD⊥CD,CD=
a,
则OF=
a,tan∠AFO=
=
,
设二面角P-BD-A的平面角为θ,则θ=∠AFO-∠PEH,
tanθ=tan(∠AFO-∠PEH)=
,即二面角P-BD-A的平面角的正切值为
.
(2)取BC中点O,
∵△ABC和△DBC是两个有公共斜边BC的直角三角形,
则OA=OB=OC=OD,
则存在以O为球心,半径R=
a的球,
设该球的内接圆柱的底面半径为x,高为y,
则有x2+
y2=2a2
令
(0<α<
),
所以该球的内接圆柱的表面积的最大值为2(1+
)πa2.
 解:(1)取BC之中点为O,连接AO,DO,
解:(1)取BC之中点为O,连接AO,DO,∵AB=AC=AD=2a
则AO⊥BC,又AB⊥AC,则BC=2
| 2 |
| 2 |
在△BCD中,∵CD=
| 6 |
则DO=
| 2 |
| ||
| 2 |
在△OAD中,∵AO2+DO2=4a2=AD2,则AO⊥DO,
又BC∩DO=O,且BC,DO?平面BCD,则AO⊥平面BCD
作PH⊥BC于H,HE⊥BD于E,连PE,
PH⊥平面BCD,PH⊥HE,得PE⊥BD,
则∠PEH是二面角P-BD-C的平面角,
设PH=x=CH,∴BH=2
| 2 |
∴EH=
| ||
| 2 |
| 2 |
| 6 |
| ||
| 2 |
∴PE=
x2+(
|
|
| ||
| 2 |
|
∵0<x≤
| 2 |
6
| ||
| 7 |
此时PH=
6
| ||
| 7 |
4
| ||
| 7 |
| PH |
| EH |
| ||
| 2 |
过点O做OF⊥BD于F,连接AF,得AF⊥BD,
则∠AFO是二面角A-BD-C的平面角,
因O为BC之中点,且BD⊥CD,CD=
| 6 |
则OF=
| ||
| 2 |
| AO |
| OF |
2
| ||
| 3 |
设二面角P-BD-A的平面角为θ,则θ=∠AFO-∠PEH,
tanθ=tan(∠AFO-∠PEH)=
| ||
| 12 |
| ||
| 12 |
(2)取BC中点O,
∵△ABC和△DBC是两个有公共斜边BC的直角三角形,
则OA=OB=OC=OD,
则存在以O为球心,半径R=
| 2 |
设该球的内接圆柱的底面半径为x,高为y,
则有x2+
| 1 |
| 4 |
令
|
| π |
| 2 |
|
所以该球的内接圆柱的表面积的最大值为2(1+
| 5 |
点评:本题考查二面角P-BD-A的平面角的正切值的求法,考查球的内接圆柱的表面积的最大值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
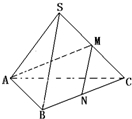 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
A、
| ||
| B、9π | ||
| C、12π | ||
| D、16π |
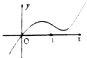 设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则
设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
设x,y都是正数,且2x+y=1,则
+
的最小值是( )
| 1 |
| x |
| 1 |
| y |
A、4
| ||
B、3
| ||
C、2+3
| ||
D、3+2
|