题目内容
过点A(-1,-2)且与椭圆
+
=1有相同焦点的双曲线的标准方程是 .
| x2 |
| 6 |
| y2 |
| 9 |
考点:双曲线的标准方程,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知设双曲线方程为
-
=1,把A(-1,-2)代入,能求出双曲线的标准方程.
| y2 |
| a2 |
| x2 |
| 3-a2 |
解答:
解:∵椭圆
+
=1的焦点为F1(0,-
),F2(0,
),
∴所求双曲线的焦点为F1(0,-
),F2(0,
),
设双曲线方程为
-
=1,
把A(-1,-2)代入,得:
-
=1,
解得a2=2或a2=6(舍),
∴双曲线的标准方程为
-x2=1.
故答案为:
-x2=1.
| x2 |
| 6 |
| y2 |
| 9 |
| 3 |
| 3 |
∴所求双曲线的焦点为F1(0,-
| 3 |
| 3 |
设双曲线方程为
| y2 |
| a2 |
| x2 |
| 3-a2 |
把A(-1,-2)代入,得:
| 4 |
| a2 |
| 1 |
| 3-a2 |
解得a2=2或a2=6(舍),
∴双曲线的标准方程为
| y2 |
| 2 |
故答案为:
| y2 |
| 2 |
点评:本题考查双曲线标准方程的求法,是基础题,解题时要认真审题,注意双曲线和椭圆性质的合理运用.

练习册系列答案
相关题目
在△ABC中,a=2,A=45°,若此三角形有两解,则b的范围为( )
A、2<b<2
| ||||
| B、b>2 | ||||
| C、b<2 | ||||
D、
|
若f(lgx)=x,则f(3)=( )
| A、103 |
| B、3 |
| C、lg3 |
| D、310 |
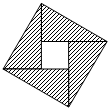 三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释.
三国时期赵爽在《勾股方圆图注》中对勾股定理的证明可用现代数学表述为如图所示,我们教材中利用该图作为“( )”的几何解释.| A、如果a>b,b>c,那么a>c |
| B、如果a>b>0,那么a2>b2 |
| C、对任意实数a和b,有a2+b2≥2ab,当且仅当a=b时等号成立 |
| D、如果a>b,c>0那么ac>bc |
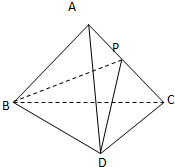 已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=
已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=