题目内容
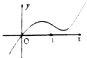 设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则
设R上的函数f(x)满足f(4)=1,它的导函数的图象如图,若正数a、b满足f(2a+b)<1,则| b+2 |
| a+2 |
A、(
| ||||
B、(-∞,
| ||||
C、(
| ||||
| D、(-∞,-3) |
考点:函数的图象
专题:函数的性质及应用
分析:先根据导函数的图象判断原函数的单调性,从而确定a、b的范围得到答案.
解答:
 解:由图可知,当x>0时,导函数f′(x)>0,原函数单调递增
解:由图可知,当x>0时,导函数f′(x)>0,原函数单调递增
∵两正数a,b满足f(2a+b)<1,
∴0<2a+b<4,
∴b,a满足不等式
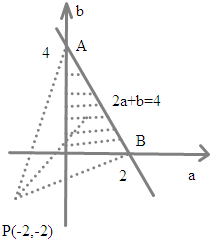
,其对应的区域如图阴影部分(不包括边界)
∴
表示过点P(-2,-2)与区域内一点M连线的斜率
由图知,当点M在A时,
取到最大值为3,当点M在点B时,
取到最小值
由于区域不包括边界,故
的取值范围是(
,3),
故选:C
 解:由图可知,当x>0时,导函数f′(x)>0,原函数单调递增
解:由图可知,当x>0时,导函数f′(x)>0,原函数单调递增∵两正数a,b满足f(2a+b)<1,
∴0<2a+b<4,
∴b,a满足不等式
|
∴
| b+2 |
| a+2 |
由图知,当点M在A时,
| b+2 |
| a+2 |
| b+2 |
| a+2 |
由于区域不包括边界,故
| b+2 |
| a+2 |
| 1 |
| 2 |
故选:C
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,根据导函数的符号判定函数的单调性是解题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据表格内的数据,可以断定方程ex-x-2=0的一个根所在的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.08 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
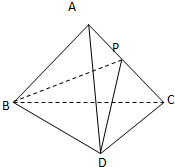 已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=
已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=