题目内容
某工厂为提高生产效益,决定对一条生产线进行升级改造,该生产线升级改造后的生产效益y万元与升级改造的投入x(x>10)万元之间满足函数关系:y=mlnx-
x2+
x+ln10(其中m为常数)若升级改造投入20万元,可得到生产效益为35.7万元.试求该生产线升级改造后获得的最大利润.(利润=生产效益-投入)(参考数据:ln2=0.7,ln5=1.6)
| 1 |
| 100 |
| 101 |
| 50 |
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:由题意,代入(20,35.7)可得35.7=mln20-4+
×20+ln10,从而求出m,计算利润函数,利用求导法求函数的最大值,从而得到最大利润.
| 101 |
| 50 |
解答:
解:由题意可得,
35.7=mln20-4+
×20+ln10,
解得,m=-1,
则y=-lnx-
x2+
x+ln10,(x>10)
设利润为f(x)=y-x
=-lnx-
x2+
x+ln10-x
=-lnx-
x2+
x+ln10,(x>10)
易得,
f′(x)=-
-
+
=
,
又∵x>10,
∴当10<x<50时,f′(x)>0,
当x>50时,f′(x)<0,
则x=50时,函数f(x)有最大值,
即f(50)=-ln50-
×(50)2+
×50+ln10=24.4(万元)
答:该生产线升级改造后获得的最大利润为24.4万元.
35.7=mln20-4+
| 101 |
| 50 |
解得,m=-1,
则y=-lnx-
| 1 |
| 100 |
| 101 |
| 50 |
设利润为f(x)=y-x
=-lnx-
| 1 |
| 100 |
| 101 |
| 50 |
=-lnx-
| 1 |
| 100 |
| 51 |
| 50 |
易得,
f′(x)=-
| 1 |
| x |
| x |
| 50 |
| 51 |
| 50 |
| (x-50)(x-1) |
| 50x |
又∵x>10,
∴当10<x<50时,f′(x)>0,
当x>50时,f′(x)<0,
则x=50时,函数f(x)有最大值,
即f(50)=-ln50-
| 1 |
| 100 |
| 51 |
| 50 |
答:该生产线升级改造后获得的最大利润为24.4万元.
点评:本题考查了学生将实际问题转化为数学问题的能力,及函数的最值的求法,属于中档题.

练习册系列答案
相关题目
根据表格内的数据,可以断定方程ex-x-2=0的一个根所在的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.08 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
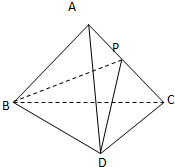 已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=
已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=