题目内容
设集合M={(x,y)|(x+1)2+y2=1,x,y∈R},N={(x,y)|x+y-c≥0,x,y∈R},则使得M∩N=M的c的取值范围是( )
A、[-
| ||
B、(-∞,-
| ||
C、[
| ||
D、(-∞,-
|
考点:集合的包含关系判断及应用
专题:集合
分析:集合M表示圆,集合N表示平面区域,画出图形,由数形结合知识,得出c的取值范围.
解答:
解:集合M={(x,y)|(x+1)2+y2=1,x,y∈R},表示以(-1,0)为圆心,1为半径的圆,
集合N={(x,y)|x+y-c≥0,x,y∈R}表示直线x+y-c=0的左上方的平面区域且包含直线;
画出图形, ;
;
数形结合知,由圆心(-1,0)到直线x+y-c=0的距离d≥r=1,
即
≥1,
解得c≥
-1或c≤-
-1,
由题意知,c≤-
-1;
故答案为:B.
集合N={(x,y)|x+y-c≥0,x,y∈R}表示直线x+y-c=0的左上方的平面区域且包含直线;
画出图形,
 ;
; 数形结合知,由圆心(-1,0)到直线x+y-c=0的距离d≥r=1,
即
| |-1+0-c| | ||
|
解得c≥
| 2 |
| 2 |
由题意知,c≤-
| 2 |
故答案为:B.
点评:本题考查了集合所表示的平面区域问题,解题时数形结合,容易得出结果.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
若不等式
<1对于一切实数都成立,则k的取值范围是( )
| 2x2+2kx+k |
| 4x2+6x+3 |
| A、(-∞,+∞) |
| B、(1,3) |
| C、(-∞,3) |
| D、(-∞,1)∪(3,+∞) |
直线y=ax+b过第一、三、四象限,则圆(x+a)2+(y+b)2=r2(r>0)的圆心在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知随机变量X~B(6,0.4),则当η=-2X+1时,D(η)=( )
| A、-1.88 | B、-2.88 |
| C、5.76 | D、6.76 |
设集合M={x|0<x≤3},N={x|x(x-2)<0},那么“a∈M”是“a∈N”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
点P是函数y=x2-2lnx的图象上任意一点,则点P到直线y=3x-1的最小距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
掷两颗均匀的大小不同的骰子,记“两颗骰子的点数和为10”为事件A,“小骰子出现的点数大于大骰子出现的点数”为事件B,则P(B|A)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
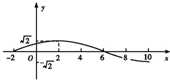 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<