题目内容
已知关于x的不等式
≥x的解集区间长度为4|a|,则实数a= .
| x+a |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:由题意得x2-x-a≤0,设方程x2-x-a=0的两个根为:x1,x2,结合|x1-x2|=4|a|,得到16a2-4a-1=0,解出a的值即可.
解答:
解:由
≥x,得:x2-x-a≤0,
设方程x2-x-a=0的两个根为:x1,x2,
∴x1+x2=1,1x1•x2=-a,
∵|x1-x2|=4|a|,
∴(x1+x2)2-4x1 x2=16a2,
∴16a2-4a-1=0,解得:a=
,
故答案为:
.
| x+a |
设方程x2-x-a=0的两个根为:x1,x2,
∴x1+x2=1,1x1•x2=-a,
∵|x1-x2|=4|a|,
∴(x1+x2)2-4x1 x2=16a2,
∴16a2-4a-1=0,解得:a=
1±
| ||
| 8 |
故答案为:
1±
| ||
| 8 |
点评:本题考查了解不等式问题,考查了一元二次方程的根与系数的关系,是一道中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知函数f(x)=
,则f(f(
))=( )
|
| π |
| 4 |
| A、1 | B、-2 | C、2 | D、-1 |
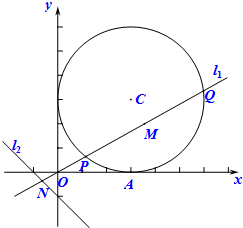 已知圆C:(x-3)2+(y-3)2=9,直线l1:y=kx与圆C交于P、Q两个不同的点,M为P、Q的中点.
已知圆C:(x-3)2+(y-3)2=9,直线l1:y=kx与圆C交于P、Q两个不同的点,M为P、Q的中点.