题目内容
已知函数f（x）=
，则f（f（
））=（ ）
|
| π |
| 4 |
| A、1 | B、-2 | C、2 | D、-1 |
考点：分段函数的应用,函数的值
专题：函数的性质及应用
分析：直接利用分段函数，利用由里及外逐步求解即可．
解答：
解：函数f（x）=
，
则f（
）=-tan
=-1．
f（f（
））=f（-1）=2×（-1）3=-2．
故选：B．
|
则f（
| π |
| 4 |
| π |
| 4 |
f（f（
| π |
| 4 |
故选：B．
点评：本题考查分段函数的应用，函数值的求法，基本知识的考查．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
如图，在正方形ABCD中，E为AB的中点，P为线段BD上的任意一点，设向量
为了了解某同学的数学学习情况，对他的6次数学测试成绩（满分100分）进行统计，作出的茎叶图如图所示，则下列关于该同学数学成绩的说法正确的是（ ）| A、中位数为83 |
| B、众数为85 |
| C、平均数为85 |
| D、方差为19 |
已知m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若m∥n，m⊥α，n?β，则α⊥β |
| C、若m∥α，m∥β，则α∥β |
| D、若m∥α，α⊥β，则m⊥β |
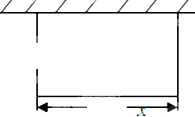某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为x米，钢筋网的总长度为y米．