Question

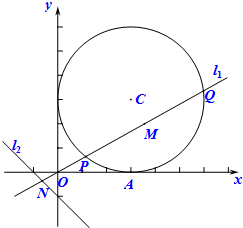已知圆C：（x-3）²+（y-3）²=9，直线l₁：y=kx与圆C交于P、Q两个不同的点，M为P、Q的中点．
（Ⅰ）已知A（3，0），若

AP

•

AQ

=0，求实数k的值；
（Ⅱ）求点M的轨迹方程；
（Ⅲ）若直线l₁与l₂：x+y+1=0的交点为N，求证：|OM|•|ON|为定值．

Answer 1

考点：直线和圆的方程的应用

专题：平面向量及应用,直线与圆

分析：（Ⅰ）首先根据向量的数量积得知直线必过圆心，从而确定直线的方程．
（Ⅱ）利用直线和弦心距所在的直线从而确定直线垂直，转化为向量的充要条件，从而求得结果，同时要注意条件．
（Ⅲ）要求|OM|•|ON|为定值首先确定|OM|=

1+k2

•

3(k+1)

k2+1

，进一步求出|ON|=

1+k2

1+k

，最后求出结果．

解答： 解：（Ⅰ）

AP

•

AQ

=0  即

AP

⊥

AQ

，
因为点A在圆C上
故直线l₁过圆心C（3，3），
解得：k=1；
（Ⅱ）设M（x，y），则OM⊥CM，即

OM

•

CM

=0①
所以：

OM

=(x，y)，

CM

=(x-3，y-3)，
坐标代入①解得：
（x，y）•（x-3，y-3）=0，
化简得：x²-3x+y²-3y=0（x＞0，y＞0）．
（Ⅲ）设P（x₁，y₁），Q（x₂，y₂），M（x₀，y₀）将y=kx代入（x-3）²+（y-3）²=9并整理得：（k²+1）x²-6（k+1）x+9=0 则x₁，x₂为方程的两根，利用根和系数的关系：
∴x1+x2=

6(k+1)

k2+1

所以：|OM|=

x 2 0 + y 2 0

=

x02+(kx0)2

=

1+k2

•x0
=

1+k2

•

3(k+1)

k2+1

直线l₁与l₂：x+y+1=0的交点为N，解得：N(-

1

k+1

，-

k

k+1

)
所以：|ON|=

(- 1 k+1 )2+(- k k+1 )2

=

1+k2

1+k

所以：|ON|•|OM|=

1+k2

•

3(k+1)

k2+1

•

1+k2

1+k

=3（定值）

点评：本题考查的知识要点：直线的方程的求法，向量的垂直的充要条件，直线的交点的解法，直线与圆的位置关系，定值问题的确定．