题目内容
已知三角形三边a，b，c，a+c=2b，∠C=2A．则sinA= ．
考点：正弦定理的应用
专题：三角函数的求值,解三角形
分析：利用正弦定理，将a+c=2b转为角的三角函数等式，然后利用∠C=2A以及三角形的内角和转为角A的等式解之．
解答：
解：因为a+c=2b，所以sinA+sinC=2sinB=2sin（A+C）
因为∠C=2A，所以sinA+sin2A=2sin（A+2A），
所以sinA+2sinAcosA=6sinA-8sin3A，整理得8cos2A-2cosA-3=0，解得cosA=-
或
，
因为∠C=2A，所以A为锐角，cosA=
；
所以sinA=
；
故答案为：
．
因为∠C=2A，所以sinA+sin2A=2sin（A+2A），
所以sinA+2sinAcosA=6sinA-8sin3A，整理得8cos2A-2cosA-3=0，解得cosA=-
| 1 |
| 2 |
| 3 |
| 4 |
因为∠C=2A，所以A为锐角，cosA=
| 3 |
| 4 |
所以sinA=
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：本题考查了利用正弦定理、倍角公式、两角和与差的三角函数恒等变形解三角形，属于中档题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
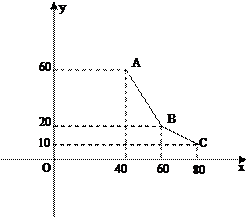小张经营某一消费品专卖店，已知该消费品的进价为每件40元，该店每月销售量y（百件）与销售单价x（元/件）之间的关系用如图的一折线表示，职工每人每月工资为1000元，该店还应交付的其它费用为每月10000元．