题目内容
已知函数f(x)=log2(x+1)+log2
.
(1)判断并证明函数f(x)的奇偶性;
(2)若关于x的方程f(x)-m=0在区间[0,1)内仅有一解,求实数m的最小值.
| 1 |
| 1-x |
(1)判断并证明函数f(x)的奇偶性;
(2)若关于x的方程f(x)-m=0在区间[0,1)内仅有一解,求实数m的最小值.
考点:对数函数图象与性质的综合应用
专题:计算题,证明题,函数的性质及应用
分析:(1)由题意可判断f(x)是奇函数,先求定义域,再确定f(x)与f(-x)的关系;
(2)由题意,f(x)=log2(-1+
),利用分离常数法求函数的值域,从而求最值.
(2)由题意,f(x)=log2(-1+
| 2 |
| 1-x |
解答:
解:(1)f(x)是奇函数,证明如下:
由题意,
,解得,x∈(-1,1),
则函数f(x)=log2(x+1)+log2
的定义域为(-1,1),
又∵f(-x)=log2(1-x)+log2
=-(log2(x+1)+log2
)=-f(x),
∴f(x)是奇函数.
(2)f(x)=log2(x+1)+log2
=log2
=log2(-1+
)
∵x∈[0,1),∴
≥2,
∴-1+
≥1,
∴m=f(x)=log2(-1+
)≥0.
故实数m的最小值为0.
由题意,
|
则函数f(x)=log2(x+1)+log2
| 1 |
| 1-x |
又∵f(-x)=log2(1-x)+log2
| 1 |
| 1+x |
| 1 |
| 1-x |
∴f(x)是奇函数.
(2)f(x)=log2(x+1)+log2
| 1 |
| 1-x |
=log2
| 1+x |
| 1-x |
| 2 |
| 1-x |
∵x∈[0,1),∴
| 2 |
| 1-x |
∴-1+
| 2 |
| 1-x |
∴m=f(x)=log2(-1+
| 2 |
| 1-x |
故实数m的最小值为0.
点评:本题考查了函数的奇偶性的证明与函数的值域的求法,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
已知函数f(x)的定义域(-1,0),则函f(2x-1)的定义域为( )
| A、(-1,1) | ||
B、(
| ||
| C、(-1,0) | ||
D、(0,
|
已知m,n是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥n,m⊥α,n?β,则α⊥β |
| C、若m∥α,m∥β,则α∥β |
| D、若m∥α,α⊥β,则m⊥β |
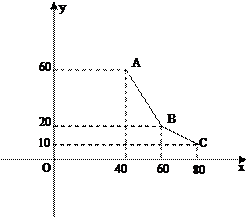 小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.
小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量y(百件)与销售单价x(元/件)之间的关系用如图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元. 如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量
如图,在正方形ABCD中,E为AB的中点,P为线段BD上的任意一点,设向量