题目内容
5.执行如图所示的程序框图,则输出的S值为( )
| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加S=0+20+21+22+23的值,并输出.
解答 解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:
该程序的作用是累加S=0+20+21+22+23的值
∵S=0+20+21+22+23=15,
故选D.
点评 本题主要考查了程序框图和算法,属于基本知识的考查.

练习册系列答案
相关题目
15.已知集合A={x|22x+1≥4},B={x|y=log2(2-x)},则A∩B=( )
| A. | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | B. | {x|x<2} | C. | $\left\{{x\left|{x≤\frac{1}{2}或x>2}\right.}\right\}$ | D. | $\left\{{x\left|{\frac{1}{2}≤x<2}\right.}\right\}$ |
13.定义在R上的奇函数f(x)满足:f(x+1)=f(x-1),且当-1<x<0时,f(x)=2x-1,则f(log220)等于( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )
| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
14.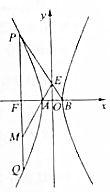 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
 已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )
已知O为坐标原点,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,A,B分别为左、右顶点,过点F做x轴的垂线交双曲线于点P,Q,连接PB交y轴于点E,连结AE交QF于点M,若M是线段QF的中点,则双曲线C的离心率为( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
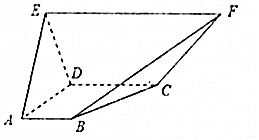 在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC=$\frac{π}{2}$,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.