题目内容
10.已知正方体ABCD-A1B1C1D1的棱长为2,长度为2的线段MN的一个端点M在棱DD1上运动,另一个端点N在正方形ABCD内运动,则MN中点的轨迹与正方体ABCD-A1B1C1D1的表面所围成的较小的几何体的体积等于$\frac{π}{6}$.分析 根据题意,连接ND,得到一个直角三角形△NMD,P为斜边MN的中点,则|PD|的长度不变,进而得到点P的轨迹是球面的一部分,求出球的半径,代入球的体积公式计算.
解答 解:如图可得,端点N在正方形ABCD内运动,连接ND,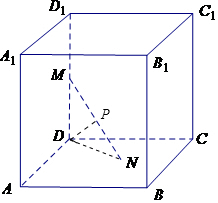
由ND,DM,MN构成一个直角三角形,
设P为MN的中点,根据直角三角形斜边上的中线长度为斜边的一半可得,
不论△MDN如何变化,P点到D点的距离始终等于1.
故P点的轨迹是一个以D为中心,半径为1的球的$\frac{1}{8}$.
其体积V=$\frac{1}{8}$×$\frac{4}{3}$×π×13=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和思维能力,解题的关键是根据P点满足的条件,判断几何体为球体的$\frac{1}{8}$,是中档题.

练习册系列答案
相关题目
5.执行如图所示的程序框图,则输出的S值为( )


| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
15.若集合P={x∈R|x>0},Q={x∈Z|(x+1)(x-4)<0},则P∩Q=( )
| A. | (0,4) | B. | (4,+∞) | C. | {1,2,3} | D. | {1,2,3,4} |
19.等比数列{an}中,a2=2,a5=$\frac{1}{4}$,则a7=( )
| A. | $\frac{1}{64}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{8}$ |
 如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.
如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q. 已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.
已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.