题目内容
13.定义在R上的奇函数f(x)满足:f(x+1)=f(x-1),且当-1<x<0时,f(x)=2x-1,则f(log220)等于( )| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{5}$ | D. | $\frac{1}{5}$ |
分析 根据对数函数的单调性,我们易判断出log220∈(4,5),结合已知中f(x+1)=f(x-1)且x∈(-1,0)时,f(x)=2x-1,利用函数的周期性与奇偶性,即可得到f(log220)的值.
解答 解:∵f(x+1)=f(x-1)
∴函数f(x)为周期为2的周期函数
又∵log232>log220>log216
∴4<log220<5
∴f(log220)=f(log220-4)=f(log2 $\frac{5}{4}$)=-f(-log2 $\frac{5}{4}$)
又∵x∈(-1,0)时,f(x)=2x-1
∴f(-log2 $\frac{5}{4}$)=-$\frac{1}{5}$,
故f(log220)=$\frac{1}{5}$.
故选:D.
点评 本题考查的知识点是函数的周期性和奇偶函数图象的对称性,其中根据已知中f(x+1)=f(x-1),求出函数的周期是解答的关键,属中档题.

练习册系列答案
相关题目
8.设i是虚数单位,复数$\frac{a+i}{1+i}$为纯虚数,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
5.执行如图所示的程序框图,则输出的S值为( )


| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=2,CF=3.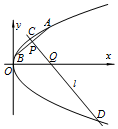 如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.
如图抛物线C:y2=4x的弦AB的中点P(2,t)(t≠0),过点P且与AB垂直的直线l与抛物线交于C、D,与x轴交于Q.