题目内容
15.已知函数f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x),x∈R,则f(x)是( )| A. | 最小正周期为π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的奇函数 | D. | 最小正周期为2π的偶函数 |
分析 利用三角函数恒等变换的应用化简函数解析式可得f(x)=-2sin2x,利用正弦函数的性质即可得解.
解答 解:∵f(x)=sin($\frac{π}{3}$-2x)-$\sqrt{3}$sin($\frac{π}{6}$+2x)
=$\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sin2x-$\sqrt{3}$($\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x)
=-2sin2x,
∴可得:T=$\frac{2π}{2}$=π,利用正弦函数的性质可得f(x)为最小正周期为π奇函数.
故选:C.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质的应用,考查了转化思想,属于基础题.

练习册系列答案
相关题目
5.执行如图所示的程序框图,则输出的S值为( )


| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
10.某经销商试销A、B两种商品一个月(30天)的记录如下:
若售出每种商品1件均获利40元,用X,Y表示售出A、B商品的日利润值(单位:元).将频率视为概率.
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(1)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(2)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.
7.已知定义在R上的奇函数f(x)满足f(x+3)=f(x),且当x∈[0,$\frac{3}{2}$)时,f(x)=一x3.则f($\frac{11}{2}$)=( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{125}{8}$ | D. | $\frac{125}{8}$ |
18.设f(x)=ex,f(x)=g(x)-h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[-1,1]时,不等式mg(x)+h(x)≥0成立,则m的最小值为( )
| A. | $\frac{{e}^{2}-1}{{e}^{2}+1}$ | B. | $\frac{2}{{e}^{2}+1}$ | C. | $\frac{{e}^{2}+1}{{e}^{2}-1}$ | D. | $\frac{1-{e}^{2}}{1+{e}^{2}}$ |
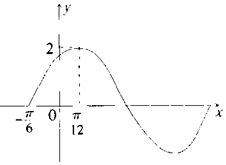 已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.
已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.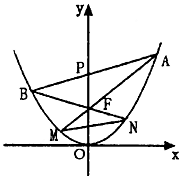 已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.
已知双曲线C1:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线为x+2y=0,且点(2,$\sqrt{2}$)在双曲线C1上.