已知集合A={x|22x+1≥4}.B={x|y=log2A．$\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$B．{x|x＜2}C．$\left\{{x\left|{x≤\frac{1}{2}或x＞2}\right.}\right\}$D．$\left\{{x\left|{\frac{1}{2}≤x＜2}\right.}\right\}$ 题目和参考答案——青夏教育精英家教网—

题目内容

15．已知集合A={x|2^2x+1≥4}，B={x|y=log₂（2-x）}，则A∩B=（　　）

A．

$\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$

B．

{x|x＜2}

C．

$\left\{{x\left|{x≤\frac{1}{2}或x＞2}\right.}\right\}$

D．

$\left\{{x\left|{\frac{1}{2}≤x＜2}\right.}\right\}$

分析求出A中x的范围确定出A，求出N中x的范围确定出B，找出两集合的交集即可．

解答解：由A中不等式变形得：2^2x+1≥4=2²，
解得：x≥$\frac{1}{2}$，即A={x|x≥$\frac{1}{2}$}，
由y=log₂（2-x），得到2-x＞0，
解得：x＜2，即B={x|x＜2}，
则A∩B={x|$\frac{1}{2}$≤x＜2}，
故选：D．

点评此题考查了交集及其运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

6．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（2$\sqrt{3}$，1），且以椭圆短轴的两个端点和一个焦点为顶点的三角形是等边三角形．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设P（x，y）是椭圆E上的动点，M（2，0）为一定点，求|PM|的最小值及取得最小值时P点的坐标．

3．

如图，菱形ABCD中，∠ABC=60°，AC与BD相交于点O，AE⊥平面ABCD，CF∥AE，AB=2，CF=3．
（1）求证：BD⊥平面ACFE；
（2）当直线FO与平面BED所成角的大小为45°时，求AE的长度．

10．已知函数f（x）=4-|x|-|x-3|
（Ⅰ）求不等式f（x+$\frac{3}{2}$）≥0的解集；
（Ⅱ）若p，q，r为正实数，且$\frac{1}{3p}$+$\frac{1}{2q}$+$\frac{1}{r}$=4，求3p+2q+r的最小值．

20．已知关于x的不等式x|x-m|-2≥m．
（1）当m=0时，求该不等式的解集；
（2）当x∈[2，3]时，该不等式恒成立，求m的取值范围．

7．

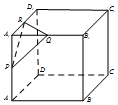正方体ABCD-A₁B₁C₁D₁的棱长为a，P，Q，R分别是棱A₁A，A₁B₁，A₁D₁的中点，以△PQR为底面作直三棱柱（侧棱与底面垂直的三棱柱叫直三棱柱），若此三棱柱另一底面的三个顶点也都在该正方体的表面上，则这个三棱柱的高为（　　）

A．

$\frac{{\sqrt{2}}}{2}$a

B．

$\sqrt{2}$a

C．

$\frac{{\sqrt{3}}}{3}$a

D．

$\frac{{\sqrt{3}}}{2}$a

4．若sin（α-$\frac{π}{6}$）=$\frac{3}{5}$，α∈（0，$\frac{π}{2}$），则cosα的值为$\frac{4\sqrt{3}-3}{10}$．

5．执行如图所示的程序框图，则输出的S值为（　　）

试题分类