题目内容
17.若将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后的图象( )| A. | 关于点$(-\frac{π}{12},0)$对称 | B. | 关于直线$x=-\frac{π}{12}$对称 | ||
| C. | 关于点$(\frac{π}{12},0)$对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,得出结论.
解答 解:将函数y=sin2x的图象向左平移$\frac{π}{6}$个单位,则平移后得到y=sin2(x+$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$)的图象,
令2x+$\frac{π}{3}$=kπ,可得x=$\frac{kπ}{2}$-$\frac{π}{6}$,故函数的图象的对称中心为($\frac{kπ}{2}$-$\frac{π}{6}$,0),k∈Z,故排除A、C;
令2x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,可得x=$\frac{kπ}{2}$+$\frac{π}{12}$,故函数的图象的对称轴方程为 x=$\frac{kπ}{2}$+$\frac{π}{12}$,k∈Z,故排除B,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
7.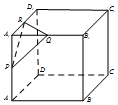 正方体ABCD-A1B1C1D1的棱长为a,P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个三棱柱的高为( )
正方体ABCD-A1B1C1D1的棱长为a,P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个三棱柱的高为( )
 正方体ABCD-A1B1C1D1的棱长为a,P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个三棱柱的高为( )
正方体ABCD-A1B1C1D1的棱长为a,P,Q,R分别是棱A1A,A1B1,A1D1的中点,以△PQR为底面作直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个三棱柱的高为( )| A. | $\frac{{\sqrt{2}}}{2}$a | B. | $\sqrt{2}$a | C. | $\frac{{\sqrt{3}}}{3}$a | D. | $\frac{{\sqrt{3}}}{2}$a |
8.设i是虚数单位,复数$\frac{a+i}{1+i}$为纯虚数,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
5.执行如图所示的程序框图,则输出的S值为( )


| A. | 1 | B. | 3 | C. | 7 | D. | 15 |
12.某公司准备将1000万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润ξ1(万元)的概率分布列如表所示:
且ξ1的期望E(ξ1)=120;若投资乙项目一年后可获得的利润ξ2(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为p(0<p<1)和1-p.若乙项目产品价格一年内调整次数X(次数)与ξ2的关系如表所示:
(Ⅰ)求m,n的值;
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
| ξ1 | 110 | 120 | 170 |
| P | m | 0.4 | n |
| X | 0 | 1 | 2 |
| ξ2 | 41.2 | 117.6 | 204.0 |
(Ⅱ)求ξ2的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求p的取值范围.
9.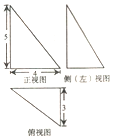 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
 《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )
《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( )| A. | 200π | B. | 50π | C. | 100π | D. | $\frac{125\sqrt{2}}{3}$π |
7.已知定义在R上的奇函数f(x)满足f(x+3)=f(x),且当x∈[0,$\frac{3}{2}$)时,f(x)=一x3.则f($\frac{11}{2}$)=( )
| A. | -$\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | -$\frac{125}{8}$ | D. | $\frac{125}{8}$ |
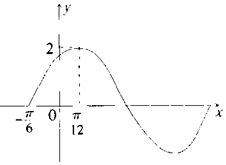 已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.
已知函数f(x)=Asin($ωx+ϕ),(ω>0,A>0,ϕ∈(0,\frac{π}{2}))$部分图象如图所示.