题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c-a)cosB-bcosA=0.
(Ⅰ)求角B的大小;
(Ⅱ)求
sinA+sin(C-
)的取值范围.
(Ⅰ)求角B的大小;
(Ⅱ)求
| 3 |
| π |
| 6 |
考点:正弦定理,两角和与差的正弦函数
专题:三角函数的求值
分析:(Ⅰ)在△ABC中,由条件利用正弦定理、两角和差的正弦公式可得 sinC(2cosB-1)=0,故有cosB=
,由此求得 B的值.
(Ⅱ)由(Ⅰ)可得
sinA+sin(C-
)=2sin(A+
),根据A∈(0,
),利用正弦函数的定义域和值域求得
sinA+sin(C-
)的取值范围.
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)可得
| 3 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 3 |
| π |
| 6 |
解答:
解:(Ⅰ)在△ABC中,∵(2c-a)cosB-bcosA=0,∴2sinCcosB-sinAcosB-sinBcosA=0,
即2sinCcosB-sin(A+B)=0,
即sinC(2cosB-1)=0,
∴cosB=
,
∴B=
.
(Ⅱ)由(Ⅰ)可得
sinA+sin(C-
)=
sinA+cosA=2sin(A+
),
∵A∈(0,
),
∴A+
∈(
,
),sin(A+
)∈(
,1],
∴2sin(A+
)∈(1,2],即
sinA+sin(C-
)的取值范围是(1,2].
即2sinCcosB-sin(A+B)=0,
即sinC(2cosB-1)=0,
∴cosB=
| 1 |
| 2 |
∴B=
| π |
| 3 |
(Ⅱ)由(Ⅰ)可得
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
∵A∈(0,
| 2π |
| 3 |
∴A+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴2sin(A+
| π |
| 6 |
| 3 |
| π |
| 6 |
点评:本题主要考查正弦定理、两角和差的正弦公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知动点P的x坐标恒为0,y坐标恒为2,则动点P的轨迹是( )
| A、平面 | B、直线 |
| C、不是平面也不是直线 | D、以上都不对 |
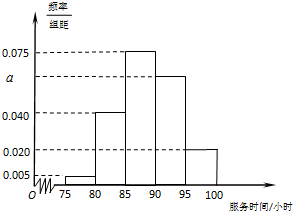 某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.