题目内容
等比数列{an}中a1=2，公比q=-2，记πn=a1×a2×…×an（即πn表示数列{an}的前n项之积），则π8，π9，π10，π11中值最大的是 ．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：等比数列{an}中a1＞0，公比q＜0，故奇数项为正数，偶数项为负数，利用新定义，即可得到结论．
解答：
解：等比数列{an}中a1＞0，公比q＜0，故奇数项为正数，偶数项为负数，
∴π11＜0，π10＜0，π9＞0，π8＞0，
∵
=a9＞1，
∴π9＞π8．
故答案为：π9．
∴π11＜0，π10＜0，π9＞0，π8＞0，
∵
| π9 |
| π8 |
∴π9＞π8．
故答案为：π9．
点评：本题考查等比数列，考查新定义，考查学生的计算能力，属于基础题．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
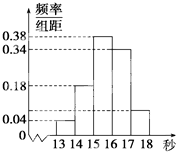为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，测试成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
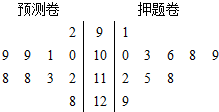四川一所学校高三年级有10名同学参加2014年北约自主招生，学校对这10名同学进行了辅导，并进行了两次模拟模拟考试，检测成绩的茎叶图如图所示．
如图所示，矩形长为5，宽为2，在矩形内随机地撒200颗黄豆，其中落在阴影部分的黄豆数位80颗，则可以估计出阴影部分的面积为