题目内容
设等差数列{an}的前n项和为Sn,公差为d.已知S2,S3+1,S4成等差数列.
(Ⅰ)求d的值;
(Ⅱ)若a1,a2,a5成等比数列,求
(n∈N*)的最大值.
(Ⅰ)求d的值;
(Ⅱ)若a1,a2,a5成等比数列,求
| an+1 |
| 2(Sn+4) |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(Ⅰ)由题意列出方程解得d;
(Ⅱ)由等差数列的通项公式及前n项和公式求得an、sn,然后利用基本不等式求得最大值.
(Ⅱ)由等差数列的通项公式及前n项和公式求得an、sn,然后利用基本不等式求得最大值.
解答:
解:(Ⅰ)由S2,S3+1,S4成等差数列得s2+s4=2s3+2,…(2分)
即(2a1+d)+(4a1+6d)=2(3a1+3d)+2,得d=2 …(5分)
(Ⅱ)由a1,a2,a5成等比数列得
=a1a5,即(a1+d)2=a1(a1+4d)
解得a1=1 …(7分)
所以an=a1+(n-1)d=2n-1,sn=
=n2…(9分)
所以
=
=
≤
…(11分)
所以,当n=2时,
的最大值为
…(12分)
即(2a1+d)+(4a1+6d)=2(3a1+3d)+2,得d=2 …(5分)
(Ⅱ)由a1,a2,a5成等比数列得
| a | 2 2 |
解得a1=1 …(7分)
所以an=a1+(n-1)d=2n-1,sn=
| n(a1+an) |
| 2 |
所以
| an+1 |
| 2(sn+4) |
| n |
| n2+4 |
| 1 | ||
n+
|
| 1 |
| 4 |
所以,当n=2时,
| an+1 |
| 2(Sn+4) |
| 1 |
| 4 |
点评:本题主要考查等差数列、等比数列的性质及求和公式知识,考查学生的运算能力及运用基本不等式求函数最值的能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,则输出的结果为( )


| A、20 | B、30 | C、40 | D、50 |
若点P在三个顶点坐标分别为C(0,0),A(0,2
),B(2,0)的△ABC内运动,则动点P到顶点A的距离|PA|<2
的概率为( )
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
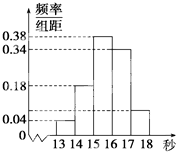 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.