题目内容
一平面截一球得到直径为2
cm的圆面，球心到这个平面的距离是2cm，则该球的体积是 ．
| 5 |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：设球心为O，截面圆心为O1，连结OO1，由球的截面圆性质和勾股定理，结合题中数据算出球半径，再利用球的体积公式即可算出答案．
解答：
解：设球心为O，截面圆心为O1，连结OO1，则OO1⊥截面圆O1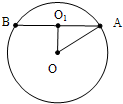
，
∵平面截一球得到直径为2
cm的圆面，球心到这个平面的距离是2cm，
∴Rt△OO1A中，O1A=
cm，OO1=2cm，
∴球半径R=OA=
=3cm，
因此球体积V=
πR3=36πcm3，
故答案为：36πcm3
，∵平面截一球得到直径为2
| 5 |
∴Rt△OO1A中，O1A=
| 5 |
∴球半径R=OA=
O
|
因此球体积V=
| 4 |
| 3 |
故答案为：36πcm3
点评：本题着重考查了球的截面圆性质、球的体积表面积公式等知识，属于基础题
练习册系列答案
相关题目