题目内容
已知函数f(x)=lnx+a,g(x)=x-a.
(Ⅰ)当直线y=g(x)恰好为曲线y=f(x)的切线时,求a的值;
(Ⅱ)当a>0时,若函数F(x)=f(x)•g(x)在区间[e-
,1]上不单调,求a的取值范围;
(Ⅲ)若a∈Z且xf(x)+g(x)>0对一切x>1恒成立,求a的最小值.
(Ⅰ)当直线y=g(x)恰好为曲线y=f(x)的切线时,求a的值;
(Ⅱ)当a>0时,若函数F(x)=f(x)•g(x)在区间[e-
| 3 |
| 2 |
(Ⅲ)若a∈Z且xf(x)+g(x)>0对一切x>1恒成立,求a的最小值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(Ⅰ)利用导数的几何意义,结合直线y=g(x)恰好为曲线y=f(x)的切线,即可求a的值;
(Ⅱ)要使F(x)=f(x)•g(x)在区间[e-
,1]上不单调,只需满足F′(e-
)=1+a+lne-
-
<0,即可求a的取值范围;
(Ⅲ)由题意x(lnx+a)+x-a>0对一切x>1成立等价于a>
对一切x>1成立.求出右边的最小值,即可求a的最小值.
(Ⅱ)要使F(x)=f(x)•g(x)在区间[e-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| a | ||
e-
|
(Ⅲ)由题意x(lnx+a)+x-a>0对一切x>1成立等价于a>
| xlnx+x |
| 1-x |
解答:
解:(Ⅰ)设切点为(x0,y0),则
∵f(x)=lnx+a,
∴f′(x)=
,
∵直线y=g(x)恰好为曲线y=f(x)的切线,
∴
=1,
∴x0=1,
∴切点为(1,a),
代入g(x)=x-a,可得1-a=a,∴a=
;
(Ⅱ)F(x)=f(x)•g(x)=(lnx+a)(x-a),
∴F′(x)=1+a+lnx-
,
∵a>0,∴在(0,+∞)上F′(x)单调递增,
∵F′(1)=1+a+ln1-a>0,
∴要使F(x)=f(x)•g(x)在区间[e-
,1]上不单调,
∴只需满足F′(e-
)=1+a+lne-
-
<0,
解得a>
;
(Ⅲ)由题意x(lnx+a)+x-a>0对一切x>1成立等价于a>
对一切x>1成立,
记h(x)=
(x>1),则h′(x)=
,
记m(x)=2+lnx-x(x>1),则m′(x)=
-1<0,
∴m(x)=2+lnx-x在(1,+∞)上单调递减,
∵m(3)=2+ln3-3>0,m(4)=ln4-2<0,
∴?x0∈(3,4),使得m(x0)=0
且x∈(1,x0),m(x)>0,h′(x)>0,h(x)在(1,x0)上单调递增;
x∈(x0,+∞),m(x)<0,h′(x)<0,h(x)在(x0,+∞)上单调递减;
∴h(x)min=h(x0)=
,
∵m(x0)=0,∴2+lnx0-x0=0,∴lnx0=x0-2,
∴h(x0)=
=-x0,
∴a>-x0,
∵x0∈(3,4),
∴-x0∈(-4,-3),
∵a∈Z,
∴a的最小值为-3.
∵f(x)=lnx+a,
∴f′(x)=
| 1 |
| x |
∵直线y=g(x)恰好为曲线y=f(x)的切线,
∴
| 1 |
| x0 |
∴x0=1,
∴切点为(1,a),
代入g(x)=x-a,可得1-a=a,∴a=
| 1 |
| 2 |
(Ⅱ)F(x)=f(x)•g(x)=(lnx+a)(x-a),
∴F′(x)=1+a+lnx-
| a |
| x |
∵a>0,∴在(0,+∞)上F′(x)单调递增,
∵F′(1)=1+a+ln1-a>0,
∴要使F(x)=f(x)•g(x)在区间[e-
| 3 |
| 2 |
∴只需满足F′(e-
| 3 |
| 2 |
| 3 |
| 2 |
| a | ||
e-
|
解得a>
| ||
| 2(e-1) |
(Ⅲ)由题意x(lnx+a)+x-a>0对一切x>1成立等价于a>
| xlnx+x |
| 1-x |
记h(x)=
| xlnx+x |
| 1-x |
| 2+lnx-x |
| (1-x)2 |
记m(x)=2+lnx-x(x>1),则m′(x)=
| 1 |
| x |
∴m(x)=2+lnx-x在(1,+∞)上单调递减,
∵m(3)=2+ln3-3>0,m(4)=ln4-2<0,
∴?x0∈(3,4),使得m(x0)=0
且x∈(1,x0),m(x)>0,h′(x)>0,h(x)在(1,x0)上单调递增;
x∈(x0,+∞),m(x)<0,h′(x)<0,h(x)在(x0,+∞)上单调递减;
∴h(x)min=h(x0)=
| x0lnx0+x0 |
| 1-x0 |
∵m(x0)=0,∴2+lnx0-x0=0,∴lnx0=x0-2,
∴h(x0)=
| x0lnx0+x0 |
| 1-x0 |
∴a>-x0,
∵x0∈(3,4),
∴-x0∈(-4,-3),
∵a∈Z,
∴a的最小值为-3.
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的最值,考查学生分析解决问题的能力,难度大.

练习册系列答案
相关题目
已知F1,F2为双曲线
-
=1(a>0,b>0)的左右焦点,M为此双曲线上的一点,满足|MF1|=3|MF2|,那么此双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) |
| B、(1,2] |
| C、(0,2) |
| D、[2,+∞) |
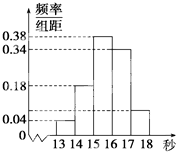 为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
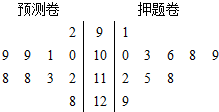 四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.
四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.