题目内容
在△ABC中,角A,B,C对应边分别是a,b,c,c=2,sin2A+sin2B-sin2C=sinAsinB.
(1)若sinC+sin(B-A)=2sin2A,求△ABC面积;
(2)求AB边上的中线长的取值范围.
(1)若sinC+sin(B-A)=2sin2A,求△ABC面积;
(2)求AB边上的中线长的取值范围.
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式利用正弦定理化简,再利用余弦定理表示出cosC,将得出关系式代入求出cosC的值,确定出C的度数,sinC+sin(B-A)=2sin2A化简后,根据cosA为0与cosA不为0两种情况,分别求出三角形ABC面积即可;
(2)根据CD为AB边上的中线,得到
=
,两边平方并利用平面向量的数量积运算法则变形得到关系式,利用余弦定理列出关系式,将cosC与c的值代入得到关系式,代入计算即可确定出|CD|的范围.
(2)根据CD为AB边上的中线,得到
| CD |
| ||||
| 2 |
解答:
解:(1)由sin2A+sin2B-sin2C=sinAsinB,利用正弦定理化简得:a2+b2-c2=ab,
∴cosC=
=
=
,即C=
,
∵sinC+sin(B-A)=sin(B+A)+sin(B-A)=2sin2A,
∴sinBcosA=2sinAcosA,
当cosA=0,即A=
,此时S△ABC=
;
当cosA≠0,得到sinB=2sinA,利用正弦定理得:b=2a,此时此时S△ABC=
;
(2)∵
=
,
∴|CD|2=
=
,
∵cosC=
,c=2,
∴由余弦定理得:c2=a2+b2-2abcosC,即a2+b2-ab=4,
∴|CD|2=
=
>1,且|CD|2=
≤3,
则|CD|的范围为(1,
].
∴cosC=
| a2+b2-c2 |
| 2ab |
| ab |
| 2ab |
| 1 |
| 2 |
| π |
| 3 |
∵sinC+sin(B-A)=sin(B+A)+sin(B-A)=2sin2A,
∴sinBcosA=2sinAcosA,
当cosA=0,即A=
| π |
| 2 |
2
| ||
| 3 |
当cosA≠0,得到sinB=2sinA,利用正弦定理得:b=2a,此时此时S△ABC=
2
| ||
| 3 |
(2)∵
| CD |
| ||||
| 2 |
∴|CD|2=
a2+b2+2abcos
| ||
| 4 |
| a2+b2+ab |
| 4 |
∵cosC=
| 1 |
| 2 |
∴由余弦定理得:c2=a2+b2-2abcosC,即a2+b2-ab=4,
∴|CD|2=
| a2+b2+ab |
| 4 |
| 4+2ab |
| 4 |
| 4+2ab |
| 4 |
则|CD|的范围为(1,
| 3 |
点评:此题考查了正弦、余弦定理,平面向量的数量积运算,熟练掌握定理是解本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
下列四个命题中,不正确的命题是( )
| A、如果一条直线与两条平行直线中的一条垂直,那么也和另一条垂直 |
| B、已知直线a、b、c,a∥b,c与a、b都不相交,若c与a所成的角为θ,则c与b所成的角也等于θ |
| C、如果空间四个点不共面,则四个点中可能有三个点共线 |
| D、若直线a∥平面α,点P∈α,则过P作a的平行线一定在α内 |

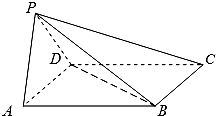 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB=
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠BAD=45°,AD=1,AB= 如图所示,矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,其中落在阴影部分的黄豆数位80颗,则可以估计出阴影部分的面积为
如图所示,矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,其中落在阴影部分的黄豆数位80颗,则可以估计出阴影部分的面积为