题目内容
已知动点P的x坐标恒为0，y坐标恒为2，则动点P的轨迹是（ ）
| A、平面 | B、直线 |
| C、不是平面也不是直线 | D、以上都不对 |
考点：与直线有关的动点轨迹方程
专题：规律型,空间位置关系与距离
分析：利用动点P的x坐标恒为0，y坐标恒为2，可得动点P的轨迹表示yoz平面内的直线y=2，从而可得结论．
解答：
解：∵动点P的x坐标恒为0，y坐标恒为2，
∴动点P的轨迹表示yoz平面内的直线y=2．
故选：B．
∴动点P的轨迹表示yoz平面内的直线y=2．
故选：B．
点评：本题考查轨迹方程，考查学生的理解能力，比较基础．
练习册系列答案
相关题目
已知斜率为k=1的直线与双曲线
-
=1（a＞0，b＞0）交于A、B两点，若A、B的中点为M（1，3），则双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、x±
| ||
B、
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
执行如图所示的程序框图，则输出的结果为（ ）
| A、20 | B、30 | C、40 | D、50 |
已知F1，F2为双曲线
-
=1（a＞0，b＞0）的左右焦点，M为此双曲线上的一点，满足|MF1|=3|MF2|，那么此双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） |
| B、（1，2] |
| C、（0，2） |
| D、[2，+∞） |
下列四个命题中，不正确的命题是（ ）
| A、如果一条直线与两条平行直线中的一条垂直，那么也和另一条垂直 |
| B、已知直线a、b、c，a∥b，c与a、b都不相交，若c与a所成的角为θ，则c与b所成的角也等于θ |
| C、如果空间四个点不共面，则四个点中可能有三个点共线 |
| D、若直线a∥平面α，点P∈α，则过P作a的平行线一定在α内 |
如图所示的流程图，若输入x的值为2，则输出x的值为（ ）
| A、5 | B、7 | C、125 | D、127 |
若点P在三个顶点坐标分别为C（0，0），A（0，2
），B（2，0）的△ABC内运动，则动点P到顶点A的距离|PA|＜2
的概率为（ ）
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
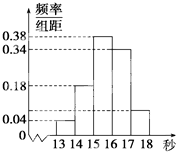为调查某市学生百米运动成绩，从该市学生中按照男女生比例随机抽取50名学生进行百米测试，测试成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．