题目内容
11.在某大学自主招生的面试中,考生要从规定的6道科学题,4道人文题共10道题中,随机抽取3道作答,每道题答对得10分,答错或不答扣5分,已知甲、乙两名考生参加面试,甲只能答对其中的6道科学题,乙答对每道题的概率都是$\frac{2}{3}$,每个人答题正确与否互不影响.(1)求考生甲得分X的分布列和数学期望EX;
(2)求甲,乙两人中至少有一人得分不少于15分的概率.
分析 (1)设学生甲得分X的所有取值为-15,0,15,30,分别求出相应的概率,由此能求出甲得分X的分布列为和EX.
(2)记事件A:“甲得分不少于15分”,记事件B:“乙得分不少于15分”.甲、乙两人中至少有一人得分大于等于15分的概率为$P=1-P(\bar A•\bar B)=1-(1-P(A))(1-P(B))$.由此能求出结果.
解答 解:(1)设学生甲得分X的所有取值为-15,0,15,30,
$P(X=-15)=\frac{C_6^0C_4^3}{{C_{10}^3}}=\frac{1}{30}$,
$P(X=0)=\frac{C_6^1C_4^2}{{C_{10}^3}}=\frac{3}{10}$,
$P(X=15)=\frac{C_6^2C_4^1}{{C_{10}^3}}=\frac{1}{2}$,
$P(X=30)=\frac{C_6^3C_4^0}{{C_{10}^3}}=\frac{1}{6}$.
∴甲得分X的分布列为
| X | -15 | 0 | 15 | 30 |
| P | $\frac{1}{30}$ | $\frac{3}{10}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
(2)记事件A:“甲得分不少于15分”,
记事件B:“乙得分不少于15分”.
$P(A)=P(X=15)+P(X=30)=\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$,
$P(B)=C_3^2×{(\frac{2}{3})^2}×\frac{1}{3}+C_3^3×{(\frac{2}{3})^3}=\frac{20}{27}$.
所以甲、乙两人中至少有一人得分大于等于15分的概率为:$P=1-P(\bar A•\bar B)=1-(1-P(A))(1-P(B))=1-\frac{7}{27}×\frac{1}{3}=\frac{74}{81}$.
点评 本题考查离散型随机变量的分布列、数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、是中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.集合A={x|y=lg(x-2)},B={y|y=2x,x≥0},则(∁RA)∩B=( )
| A. | (0,2) | B. | [0,2] | C. | [1,2] | D. | (1,2) |
1.设二次函数f(x)=ax2+bx+c(a≠0)中的a、b均为整数,且f(0)、f(1)均为奇数,则( )
| A. | 方程f(x)=0有两个不相等的整数根 | B. | 方程f(x)=0没有整数根 | ||
| C. | 方程f(x)=0至少有一个整数根 | D. | 方程f(x)=0至多有一个整数根 |
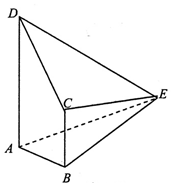 如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.
如图,在四棱锥E-ABCD中,平面CDE⊥平面ABCD,∠DAB=∠ABC=90°,AB=BC=1,AD=ED=3,EC=2.