题目内容
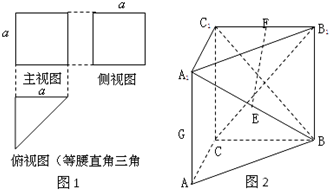 一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.
一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.(1)求证:B1C⊥平面A1BC1;
(2)求证:EF∥平面ACC1A1;
(3)在BB1上是否存在一点M,使得GM+MC的长最短.若存在,求出这个最短值,并指出点M的位置;若不存在,请说明理由.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)利用直三棱柱的性质,只要证明B1C垂直与平面A1BC1的两条相交直线;
(2)连接A1C,AC1交于点O,连接OE,利用中位线的性质得到四边形OEFG为平行四边形,再由线面平行的判定定理可得;
(3)在BB1上存在一点M,使得GM+MC的长最短.通过勾股定理求得.
(2)连接A1C,AC1交于点O,连接OE,利用中位线的性质得到四边形OEFG为平行四边形,再由线面平行的判定定理可得;
(3)在BB1上存在一点M,使得GM+MC的长最短.通过勾股定理求得.
解答:
 (1)证明:∵AA1⊥平面ABC,AA1∥CC1,
(1)证明:∵AA1⊥平面ABC,AA1∥CC1,
∴CC1⊥平面ABC,
∴CC1⊥AC,∵AC⊥BC,
∴AC⊥平面BCC 1B 1,…(2分)
∵AC∥A1C1,
∴A1C1⊥平面BCC 1B 1,
∴A1C1⊥B1C…(3分)
又B1C⊥BC1,A1C1∩BC1=C1,
∴B1C⊥平面A1BC1…(5分)
(2)连接A1C,AC1交于点O,连接OE…(6分)
由题意可得,O为A1C中点,
因为E为A1B中点,∴OE∥
CB并且OE=
CB
因为F为C1B1的中点中点,∴C1F∥
CB,C1F=
CB
∴OE∥C1F,OE=C1F
∴四边形OEFG为平行四边形…(8分)
∴FE∥OC1…(9分)
∵FE?平面ACC1A1,OC1?平面ACC1A1,
∴FE∥平面ACC1A1…(10分)
(3)在BB1上存在一点M,使得GM+MC的长最短,此时沿CC1展开,时G,M,C在一条直线上.
最短值为GC=
=
a
此时BM=
a…(14分)
 (1)证明:∵AA1⊥平面ABC,AA1∥CC1,
(1)证明:∵AA1⊥平面ABC,AA1∥CC1,∴CC1⊥平面ABC,
∴CC1⊥AC,∵AC⊥BC,
∴AC⊥平面BCC 1B 1,…(2分)
∵AC∥A1C1,
∴A1C1⊥平面BCC 1B 1,
∴A1C1⊥B1C…(3分)
又B1C⊥BC1,A1C1∩BC1=C1,
∴B1C⊥平面A1BC1…(5分)
(2)连接A1C,AC1交于点O,连接OE…(6分)
由题意可得,O为A1C中点,
因为E为A1B中点,∴OE∥
| 1 |
| 2 |
| 1 |
| 2 |
因为F为C1B1的中点中点,∴C1F∥
| 1 |
| 2 |
| 1 |
| 2 |
∴OE∥C1F,OE=C1F
∴四边形OEFG为平行四边形…(8分)
∴FE∥OC1…(9分)
∵FE?平面ACC1A1,OC1?平面ACC1A1,
∴FE∥平面ACC1A1…(10分)
(3)在BB1上存在一点M,使得GM+MC的长最短,此时沿CC1展开,时G,M,C在一条直线上.
最短值为GC=
(a+
|
| ||||
| 2 |
此时BM=
| ||
| 2 |
点评:本题考查了直三棱柱的性质、线面平行的判定定理以及线段最短问题,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
随机写出两个小于1的正数x与y,它们与数1一起形成一个三元数组(x,y,1).这样的三元数组正好是
一个钝角三角形的三边的概率是( )
一个钝角三角形的三边的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=(
)
的值域为( )
| 1 |
| 3 |
| x-1 |
| A、(-∞,0) | B、(0,1] |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、若p∨q为真命题,则p,q均为真命题 |
| C、命题“存在x∈R,使得x2+x+1<0”的否定是:“对任意x∈R,均有x2+x+1<0” |
| D、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
设单位向量
,
,
满足:
•
=0,存在实数x,y使得
=x
+y
,则实数x+y的取值范围是( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、[-1,1] | ||||
| B、[0,1] | ||||
C、[-
| ||||
D、[0,
|
 如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.
如图,四棱锥P-ABCD的底面ABCD是边长为a的正方形,PA⊥平面ABCD,点E是PA的中点.