题目内容
随机写出两个小于1的正数x与y,它们与数1一起形成一个三元数组(x,y,1).这样的三元数组正好是
一个钝角三角形的三边的概率是( )
一个钝角三角形的三边的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据几何概型的概率公式,求出这个三元组正好是钝角三角形的三个边的等价条件,即可得到结论.
解答:
 解:这个三元组正好是钝角三角形的三个边,应满足一下条件:cosθ=
解:这个三元组正好是钝角三角形的三个边,应满足一下条件:cosθ=
<0,即x2+y2<1,
,对应的区域如图,
则圆面积的
为
,
直线和区域围城的面积是
,
弓形的面积为
-
,
总区域的面积为:1
则这个三元组正好是钝角三角形的三个边的概率P=
-
.
故选:C
 解:这个三元组正好是钝角三角形的三个边,应满足一下条件:cosθ=
解:这个三元组正好是钝角三角形的三个边,应满足一下条件:cosθ=| x2+y2-1 |
| 2xy |
|
则圆面积的
| 1 |
| 4 |
| π |
| 4 |
直线和区域围城的面积是
| 1 |
| 2 |
弓形的面积为
| 1 |
| 2 |
| π |
| 4 |
总区域的面积为:1
则这个三元组正好是钝角三角形的三个边的概率P=
| π |
| 4 |
| 1 |
| 2 |
故选:C
点评:本题主要考查几何概型的概率计算,根据三角形边角关系,求出对应区域的面积是解决本题的关键

练习册系列答案
相关题目
执行如图的程序框图,则输出的结果为( )


| A、8 | B、10 | C、12 | D、14 |
若复数z满足:z=(z-1)•i,则复数z的共轭复数2
=( )
. |
| z |
| A、-i | B、i | C、1-i | D、1+i |

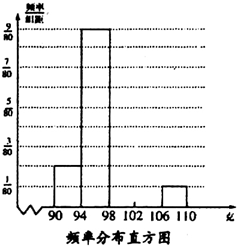 为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:
为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:

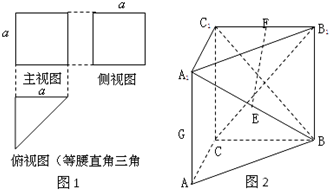 一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.
一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.