题目内容
函数y=（
）
的值域为（ ）
| 1 |
| 3 |
| x-1 |
| A、（-∞，0） | B、（0，1] |
考点：函数的值域
专题：函数的性质及应用
分析：根据复合函数的递增得出：函数y=（
）
在[1，+∞）单调递减，求出定义域为[1，+∞），即可求解值域．
| 1 |
| 3 |
| x-1 |
解答：
解：∵函数y=（
）
的定义域为[1，+∞），
∴u（x）=
单调递增，
∴根据复合函数的递增得出：函数y=（
）
在[1，+∞）单调递减，
当x=1时，y=1，（
）u＞0，
∴y大=1，
函数y=（
）
的值域为（0，1]，
故选：B．
| 1 |
| 3 |
| x-1 |
∴u（x）=
| x-1 |
∴根据复合函数的递增得出：函数y=（
| 1 |
| 3 |
| x-1 |
当x=1时，y=1，（
| 1 |
| 3 |
∴y大=1，
函数y=（
| 1 |
| 3 |
| x-1 |
故选：B．
点评：本题考查了函数的定义域，单调性，值域的求解，属于容易题，关键判断单调性．
练习册系列答案
相关题目
执行如图的程序框图，则输出的结果为（ ）
| A、8 | B、10 | C、12 | D、14 |
若复数z满足：z=（z-1）•i，则复数z的共轭复数2
=（ ）
. |
| z |
| A、-i | B、i | C、1-i | D、1+i |
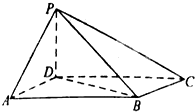如图，在四棱锥P-ABCED中，PD⊥面ABCD，四边形ABCD为平行四边形，∠DAB=60°，AB=PA=2AD=4，
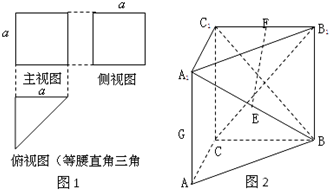一个三棱柱的三视图及直观图如图所示，E，F，G分别是A1B，B1C1，AA1的中点，AA1⊥底面ABC．已知两定点A（-1，0）和B（1，0），动点P（x，y）在直线l：y=x+2上移动，椭圆C以A，B为焦点且经过点P，则椭圆C的离心率的最大值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
