题目内容
已知sinα+
cosα=
,则tanα= .
| 2 |
| 3 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件利用辅助角公式可得sin(α+β)=1,其中,α+β=2kπ+
,k∈z,tanβ=
.再根据tanα=tan(2kπ+
-β)=cotβ,求得结果.
| π |
| 2 |
| 2 |
| π |
| 2 |
解答:
解:∵已知sinα+
cosα=
,∴
(
sinα+
cosα)=
,
∴(
sinα+
cosα)=1,即sin(α+β)=1,其中,α+β=2kπ+
,k∈z,tanβ=
.
则tanα=tan(2kπ+
-β)=cotβ=
=
,
故答案为:
| 2 |
| 3 |
| 3 |
| 1 | ||
|
| ||
|
| 3 |
∴(
| 1 | ||
|
| ||
|
| π |
| 2 |
| 2 |
则tanα=tan(2kπ+
| π |
| 2 |
| 1 | ||
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查同角三角函数间的基本关系,辅助角公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
已知两定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+2上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
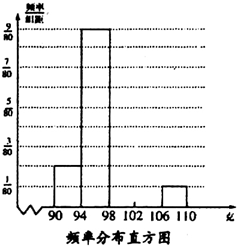 为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图:
为了解食品厂生产的一种食品中添加剂的含量,食品监管部门随机抽取了一个批次的20袋样品进行检验,获得以下频率分布表和频率分布直方图: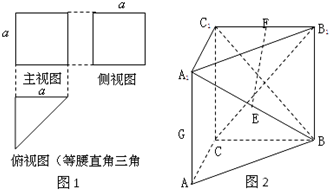 一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.
一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.