题目内容
设单位向量
,
,
满足:
•
=0,存在实数x,y使得
=x
+y
,则实数x+y的取值范围是( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| A、[-1,1] | ||||
| B、[0,1] | ||||
C、[-
| ||||
D、[0,
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:对
=x
+y
两边平方可得到x2+y2=1,所以设x=sinα,y=cosα,从而可得到x+y=
sin(α+
),从而可得出x+y的取值范围.
| c |
| a |
| b |
| 2 |
| π |
| 4 |
解答:
解:由已知条件:
2=x2
2+2xy
•
+y2
2;
∴x2+y2=1;
∴设x=sinα,y=cosα,则:
x+y=sinα+cosα=
sin(α+
);
∴-
≤x+y≤
;
∴实数x+y的取值范围是[-
,
].
故选C.
| c |
| a |
| a |
| b |
| b |
∴x2+y2=1;
∴设x=sinα,y=cosα,则:
x+y=sinα+cosα=
| 2 |
| π |
| 4 |
∴-
| 2 |
| 2 |
∴实数x+y的取值范围是[-
| 2 |
| 2 |
故选C.
点评:考查数量积的运算,sin2α+cos2α=1,以及两角和的正弦公式.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知{an}是等比数列,其前n项和为Sn,若
=9,则
=( )
| S6 |
| S3 |
| S12 |
| S6 |
| A、9 | B、18 | C、64 | D、65 |
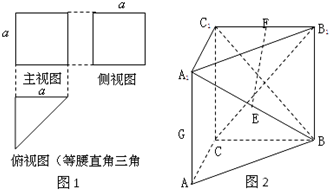 一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.
一个三棱柱的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC.