题目内容
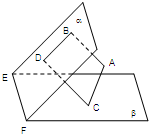 如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影
如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影在同一条直线上.那么上述三个条件中能成为增加条件的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:空间中直线与直线之间的位置关系
专题:
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①因为AC⊥β,且EF?β,所以AC⊥EF.
又AB⊥α,且EF?α,所以EF⊥AB.
因为AC∩AB=A,AC?平面ACBD,AB?平面ACBD,所以EF⊥平面ACBD,
因为BD?平面ACBD,所以BD⊥EF.
所以①可以成为增加的条件.
②若AC∥EF,则AC∥平面α,
所以BD∥AC,所以BD∥EF.
所以②不可以成为增加的条件.
AC与α,β所成的角相等,AC与EF 不一定,可以是相交、可以是平行、也可能垂直,
所以EF与平面ACDB不垂直,所以就推不出EF与BD垂直.所以②不可以成为增加的条件.
③AC与CD在β内的射影在同一条直线上
因为CD⊥α且EF?α所以EF⊥CD.
所以EF与CD在β内的射影垂直,
AC与CD在β内的射影在同一条直线上
所以EF⊥AC
因为AC∩CD=C,AC?平面ACBD,CD?平面ACBD,所以EF⊥平面ACBD,
因为BD?平面ACBD所以BD⊥EF.
所以③可以成为增加的条件.
故选:C.
又AB⊥α,且EF?α,所以EF⊥AB.
因为AC∩AB=A,AC?平面ACBD,AB?平面ACBD,所以EF⊥平面ACBD,
因为BD?平面ACBD,所以BD⊥EF.
所以①可以成为增加的条件.
②若AC∥EF,则AC∥平面α,
所以BD∥AC,所以BD∥EF.
所以②不可以成为增加的条件.
AC与α,β所成的角相等,AC与EF 不一定,可以是相交、可以是平行、也可能垂直,
所以EF与平面ACDB不垂直,所以就推不出EF与BD垂直.所以②不可以成为增加的条件.
③AC与CD在β内的射影在同一条直线上
因为CD⊥α且EF?α所以EF⊥CD.
所以EF与CD在β内的射影垂直,
AC与CD在β内的射影在同一条直线上
所以EF⊥AC
因为AC∩CD=C,AC?平面ACBD,CD?平面ACBD,所以EF⊥平面ACBD,
因为BD?平面ACBD所以BD⊥EF.
所以③可以成为增加的条件.
故选:C.
点评:本题考查能成为增加条件的命题个数的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
-
,(a∈R且a>0).
(1)判断函数f(x)的单调性,并证明;
(2)若函数f(x)的定义域为(-2,2)时,求使f(1-m)-f(m2-1)<0成立的实数m的取值范围.
| ex |
| a |
| a |
| ex |
(1)判断函数f(x)的单调性,并证明;
(2)若函数f(x)的定义域为(-2,2)时,求使f(1-m)-f(m2-1)<0成立的实数m的取值范围.
函数f(x)=2x+log2x-3在区间(1,2)内的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |
已知函数f(x)=sin(ωx-
)(ω>0)在(0,
)上单调递增,则ω的最大值为( )
| π |
| 6 |
| 4π |
| 3 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
 如图,在△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且
如图,在△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且