题目内容
函数f（x）=2x+log2x-3在区间（1，2）内的零点个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由于函数f（x）=2x+log2x-3在区间（1，2）上是增函数，且f（1）＜0，f（2）＞0，根据函数零点的判定定理可得结论．
解答：
解：由于函数f（x）=2x+log2x-3在区间（1，2）上是增函数，且f（1）=-1＜0，f（2）=2＞0，
根据函数零点的判定定理可得，函数f（x）=2x+log2x-3在区间（1，2）内的零点个数是1，
故选：B．
根据函数零点的判定定理可得，函数f（x）=2x+log2x-3在区间（1，2）内的零点个数是1，
故选：B．
点评：本题主要考查函数零点的判定定理的应用，属于基础题．
练习册系列答案
相关题目
如果f（a+b）=f（a）•f（b）且f（1）=2，则
+
+
+…+
=（ ）
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2014) |
| f(2013) |
| A、2012 | B、1007 |
| C、2014 | D、2013 |
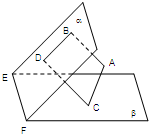如图，设平面α∩平面β=EF，AB⊥α，CD⊥α，垂足分别为B，D，如果再增加一个条件，就可以推出BD⊥EF．现有：①AC⊥β；②AC∥EF；③AC与CD在β内的射影
如图是定义在区间[-2，2]的函数y=f（x），则f（x）的减区间是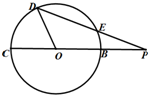
如图，割线PBC经过圆心O，OB=PB=1，又PED交圆O于E，D，且DE=