题目内容
如图，在△ABC中，∠A=60°，∠A的平分线交BC于D，若AB=4，且| AD |
| 1 |
| 4 |
| AC |
λ
| AB |
考点：向量在几何中的应用
专题：计算题,平面向量及应用
分析：因为B，D，C三点共线，所以有
+λ=1，解得λ=
，再确定
=
，
=
，AMDN是菱形，即可得出结论．
| 1 |
| 4 |
| 3 |
| 4 |
| AN |
| 1 |
| 4 |
| AC |
| AM |
| 3 |
| 4 |
| AB |
解答：
解：因为B，D，C三点共线，所以有
+λ=1，解得λ=
，如图，过点D分别作AC，AB的平行线交AB，AC于点M，N，则
=
，
=
，
∵△ABC中，∠A=60°，∠A的平分线交BC于D，
∴AMDN是菱形，
∵AB=4，∴AN=AM=3，
∴AD=3
．
故答案为：3
．
解：因为B，D，C三点共线，所以有| 1 |
| 4 |
| 3 |
| 4 |
| AN |
| 1 |
| 4 |
| AC |
| AM |
| 3 |
| 4 |
| AB |
∵△ABC中，∠A=60°，∠A的平分线交BC于D，
∴AMDN是菱形，
∵AB=4，∴AN=AM=3，
∴AD=3
| 3 |
故答案为：3
| 3 |
点评：本题考查向量在几何中的应用，考查学生的计算能力，确定AN=AM=3是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设f（x），g（x）分别是定义在（-∞，0）∪（0，+∞）上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＞0．且g（-3）=0．则不等式f（x）g（x）＜0的解集是（ ）
| A、（-3，0）∪（3，+∞） |
| B、（-3，0）∪（0，3） |
| C、（-∞，-3）∪（3，+∞） |
| D、（-∞，-3）∪（0，3） |
已知函数f（x）=4x2-mx-8在[5，20]具有单调性，则实数的取值范围为（ ）
| A、（-∞，-160]∪[160，+∞） |
| B、（-∞，40]∪[160，+∞） |
| C、（-∞，-160]∪[40，+∞） |
| D、[40，160] |
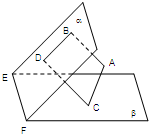如图，设平面α∩平面β=EF，AB⊥α，CD⊥α，垂足分别为B，D，如果再增加一个条件，就可以推出BD⊥EF．现有：①AC⊥β；②AC∥EF；③AC与CD在β内的射影
如图是定义在区间[-2，2]的函数y=f（x），则f（x）的减区间是