题目内容
已知函数f(x)=(x3+2x2+3x+t)e-x,t∈R.
(1)若函数y=f(x)在区间[-1,2]上为减函数,求t的取值范围.
(2)若存在实数t∈[0,2],使对任意的x∈[-5,m],不等式f(x)≤x恒成立,求整数m的最大值.
(1)若函数y=f(x)在区间[-1,2]上为减函数,求t的取值范围.
(2)若存在实数t∈[0,2],使对任意的x∈[-5,m],不等式f(x)≤x恒成立,求整数m的最大值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)先求出函数f(x)的导数,将问题转化为f′(x)<0在区间[-1,2]恒成立,令g(x)=x3+5x2+7x+t+3,只需g(x)<0在区间[-1,2]恒成立,通过求导得出g(x)在区间[-1,2]的最大值为g(2)=45+t<0即可,解出即可;
(2)问题转化为不等式0≤xex-x3-2x2-3x在x∈[-5,m]上恒成立,得不等式组
或
,令m(x)=ex,n(x)=x2+2x+3,画出函数的图象,取m的整数值代入即可求出.
(2)问题转化为不等式0≤xex-x3-2x2-3x在x∈[-5,m]上恒成立,得不等式组
|
|
解答:
解:(1)∵f′(x)=e-x(x3+5x2+7x+t+3),
若函数y=f(x)在区间[-1,2]上为减函数,
只需f′(x)<0在区间[-1,2]恒成立,
令g(x)=x3+5x2+7x+t+3,
∴只需g(x)<0在区间[-1,2]恒成立,
又g′(x)=3x2+10x+7=(3x+7)(x+1),
在[-1,2]上时,g′(x)>0,
∴g(x)在区间[-1,2]递增,
∴g(x)在区间[-1,2]的最大值为g(2)=45+t<0即可,
∴t<-45;
(2)不等式f(x)≤x,即(x3+2x2+3x+t)e-x≤x,
即t≤xex-x3-2x2-3x,
转化为存在实数t∈[0,2],使对任意的x∈[-5,m],
不等式t≤xex-x3-2x2-3x恒成立,
即不等式0≤xex-x3-2x2-3x在x∈[-5,m]上恒成立,
∴只需
或
,
令m(x)=ex,n(x)=x2+2x+3,
画出m(x),n(x)的图象,如图示:
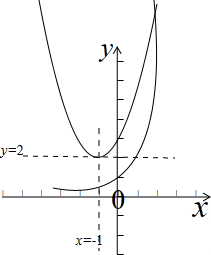 ,
,
显然m的最大值大于0,
m=1时,m(1)=e<n(1)=6,
m=2时,m(2)=e2<9<n(2)=11,
m=3时,m(3)=e3>2.73=19.86>n(3)=18,
∴满足条件的整数m的最大值是2.
若函数y=f(x)在区间[-1,2]上为减函数,
只需f′(x)<0在区间[-1,2]恒成立,
令g(x)=x3+5x2+7x+t+3,
∴只需g(x)<0在区间[-1,2]恒成立,
又g′(x)=3x2+10x+7=(3x+7)(x+1),
在[-1,2]上时,g′(x)>0,
∴g(x)在区间[-1,2]递增,
∴g(x)在区间[-1,2]的最大值为g(2)=45+t<0即可,
∴t<-45;
(2)不等式f(x)≤x,即(x3+2x2+3x+t)e-x≤x,
即t≤xex-x3-2x2-3x,
转化为存在实数t∈[0,2],使对任意的x∈[-5,m],
不等式t≤xex-x3-2x2-3x恒成立,
即不等式0≤xex-x3-2x2-3x在x∈[-5,m]上恒成立,
∴只需
|
|
令m(x)=ex,n(x)=x2+2x+3,
画出m(x),n(x)的图象,如图示:
 ,
,显然m的最大值大于0,
m=1时,m(1)=e<n(1)=6,
m=2时,m(2)=e2<9<n(2)=11,
m=3时,m(3)=e3>2.73=19.86>n(3)=18,
∴满足条件的整数m的最大值是2.
点评:本题考查了函数的单调性问题,考查了函数的最值问题,考查导数的应用,考查转化思想,数形结合思想,是一道综合题.

练习册系列答案
相关题目
正三棱柱ABC-A1B1C1的底面边长为3,侧棱AA1=
,D是CB延长线上一点,且BD=BC,则二面角B1-AD-B的大小( )
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果f(a+b)=f(a)•f(b)且f(1)=2,则
+
+
+…+
=( )
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2014) |
| f(2013) |
| A、2012 | B、1007 |
| C、2014 | D、2013 |
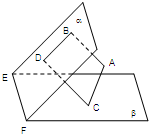 如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影
如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影