题目内容
已知函数f(x)=sin(ωx-
)(ω>0)在(0,
)上单调递增,则ω的最大值为( )
| π |
| 6 |
| 4π |
| 3 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由正弦型函数的性质,函数f(x)=sin(ωx-
)在ω>0时,可解得单调递增区间为[
,
],k∈Z,由已知函数在(0,
)上单调递增,可解得ω≤
.
| π |
| 6 |
2kπ-
| ||
| ω |
2kπ+
| ||
| ω |
| 4π |
| 3 |
| 1 |
| 2 |
解答:
解:由正弦型函数的性质,函数f(x)=sin(ωx-
),在ω>0时,单调递增区间为[
,
],k∈Z,
∵函数在(0,
)上单调递增,
∴
≤0,
≥
,k∈Z,
∴不妨取k=0,可解得ω≤
故选:A.
| π |
| 6 |
2kπ-
| ||
| ω |
2kπ+
| ||
| ω |
∵函数在(0,
| 4π |
| 3 |
∴
2kπ-
| ||
| ω |
2kπ+
| ||
| ω |
| 4π |
| 3 |
∴不妨取k=0,可解得ω≤
| 1 |
| 2 |
故选:A.
点评:本题主要考察了正弦函数的图象和性质,不等式的解法,属于基础题.

练习册系列答案
相关题目
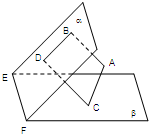 如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影
如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影在同一条直线上.那么上述三个条件中能成为增加条件的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
设f(n)=2+24+27+210+…+23n+10(n∈N),则f(n)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|