题目内容
已知函数f(x)=
+lnx-1(a>0).
(1)当a=1时,求函数f(x)的单调区间;
(2)求f(x)在x∈[
,e]上的最小值.
| a |
| x |
(1)当a=1时,求函数f(x)的单调区间;
(2)求f(x)在x∈[
| 1 |
| e |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)通过a=1,求出函数的导数,令导数大于0,小于0,即可求函数f(x)的单调区间;
(2)通过0<a≤
,
<a<e,e≤a判断导函数的单调性,然后求f(x)在x∈[
,e]上的最小值.
(2)通过0<a≤
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
解答:
(本题满分(12分),第(1)问(5分),第(2)问7分)
解:(1)f′(x)=
…(1分)
x∈(0,1)时,f′(x)<0,则f(x)在 (0,1)上单调递减,
x∈[1,+∞)时,f′(x)≥0,则f(x)在[1,+∞)上单调递增;…(5分)
(2)f′(x)=
…(6分)
①当0<a≤
时,f'(x)≥0,f(x)在x∈[
,e]单调递增,f(x)min=f(
)=ae-2,…(8分)
②当
<a<e时,f(x)在[
,a]上递减,(a,e]上单调递增,f(x)min=f(a)=lna,…(10分)
③当e≤a时,f'(x)≤0,f(x)在x∈[
,e]单调递减,f(x)min=f(e)=
.…(12分)
解:(1)f′(x)=
| x-1 |
| x2 |
x∈(0,1)时,f′(x)<0,则f(x)在 (0,1)上单调递减,
x∈[1,+∞)时,f′(x)≥0,则f(x)在[1,+∞)上单调递增;…(5分)
(2)f′(x)=
| x-a |
| x2 |
①当0<a≤
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
②当
| 1 |
| e |
| 1 |
| e |
③当e≤a时,f'(x)≤0,f(x)在x∈[
| 1 |
| e |
| a |
| e |
点评:本题考查函数的导数的综合应用,函数的单调区间的求法,利用导数求解函数的最小值的方法,考查转化思想,分类讨论思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正三棱柱ABC-A1B1C1的底面边长为3,侧棱AA1=
,D是CB延长线上一点,且BD=BC,则二面角B1-AD-B的大小( )
| 3 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果f(a+b)=f(a)•f(b)且f(1)=2,则
+
+
+…+
=( )
| f(2) |
| f(1) |
| f(4) |
| f(3) |
| f(6) |
| f(5) |
| f(2014) |
| f(2013) |
| A、2012 | B、1007 |
| C、2014 | D、2013 |
函数f(x)=log2(x+4)-3x的零点有( )
| A、0 | B、1 | C、2 | D、3 |
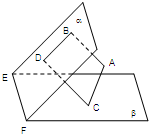 如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影
如图,设平面α∩平面β=EF,AB⊥α,CD⊥α,垂足分别为B,D,如果再增加一个条件,就可以推出BD⊥EF.现有:①AC⊥β;②AC∥EF;③AC与CD在β内的射影